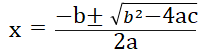【中3数学】中3で習う単元まとめ | 勉強のコツをご紹介

中学3年生の数学は、高校数学につながる重要な単元が多く出てきます。また高校入試問題にも頻出の単元ばかりです。

ここでは中3数学で学ぶ内容とおさえておきたいポイントについて解説します。

中3で習う数学の概要

中3の数学はこれまでの単元同士が複雑につながりあい、より高度な内容に発展していきます。また高校数学の土台になる内容も多く、難しくなりますが「数学らしい数学」を学べるのが醍醐味です。

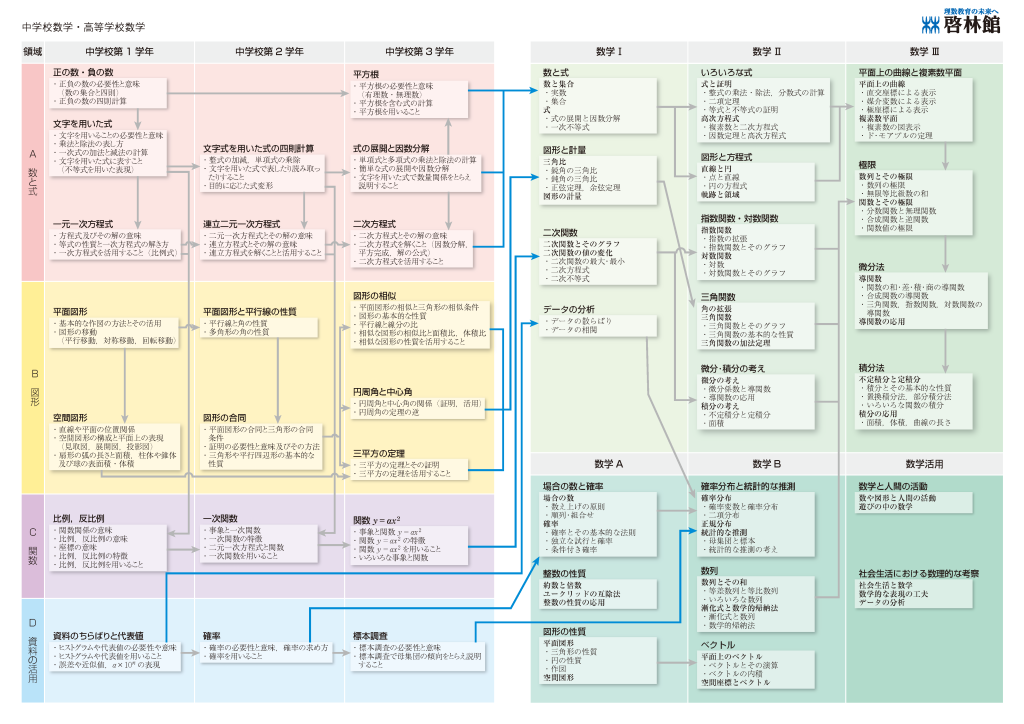
※ 新学習指導要領における算数・数学内容系統一覧表｜啓林館

上の図は教科書会社が作成した、数学の単元同士のつながりを可視化したものです。一番左に中1数学があり、続いて中2、中3と習う単元が配置されています。右半分は、高校数学の内容です。また、図中の矢印は、単元同士の関連性があることを示します。

中3数学は、中1から連綿と続く中学数学の集大成でもあり、高校数学に直結する学年といえないでしょうか。

中3の数学は「頭の使い方」が、中2までとは変わります。中2までの数学は、問題をパターン化し解法を覚えれば対応できました。難しいとされる問題も、実はいくつかの基本パターンの組み合わせに過ぎないケースも多かったのです。

しかし中3の数学では、解ける方法を見つけるまでに試行錯誤が必要な問題が増えてきます。これを「推論」といいます。パターンや公式に当てはめるだけでは解けず、「どうすれば解けるか」を自分自身で推しはかり見つけなければなりません。

頭の使い方が変わるため「急に難しくなった」と感じる中学生も多いのが、中3数学です。高校入試、そしてその先にある高校数学への土台を作っているのだと前向きに受け止め、コツコツ頑張っていきましょう。

勉強の注意点

中3の数学は「学校でいま学んでいる単元の学習」と、「これまでに習った範囲の復習」の両輪を回すことが成績アップのポイントです。2つの学習を同時に進めなければいけない理由は、2つあります。

たとえば、中3の2番目に登場する「平方根」の単元は、以下の単元に紐づきます。

・中1：正負の数、文字と式、方程式
・中2：式と計算、連立方程式
・中3：展開・因数分解

また平方根で習った知識は、次の2次方程式につながります。

過去の単元に理解が不十分な箇所があると、そこから紐づく先の内容もよくわからなくなります。結果的に理解不足が積み重なり、数学全体がわからなくなってしまうことも少なくありません。

過去の苦手単元・理解不足だと感じる箇所は、しっかり復習しましょう。

中3の定期テストでは入試を意識し、復習問題も出題されます。復習にしっかり取り組むと、定期テストの結果にも良い影響を与えます。

１．式の展開と因数分解

中1、中2で学んだ式の計算の発展事項として「展開」「因数分解」を学びます。因数分解は特に、できるようになるまで何度も繰り返しましょう。

（１）式の展開と分配法則

・展開と分配法則

「展開」とは、式にある括弧（）を開いて足し算引き算で単項式をつないだ形にすることを指します。「括弧を開く」とは、以下のように分配法則を用いてかけ算することです。

x(y＋z)＝xy＋xz　←xを、括弧の中のyとzそれぞれにかけて、足す。

・(a＋b)(c＋d)の式の展開

1次式と1次式（数字と文字が入った式も）の計算も同様に行います。

(a＋5)(b＋2)＝ab＋2a＋5b＋10　←アルファベット順、次数の高い順に並べる

・負の記号がある式の展開

負の記号が入っていると、符号が逆転するため注意して展開しましょう。

（２）乗法の公式

・(x＋a)(x＋b)の公式

上の展開を公式にしたものです。のちに因数分解のたすきがけ、証明問題などでも利用します。

・平方の公式

展開をすればいいと考える中学生がいますが、この公式は次の因数分解で利用するため覚えましょう。

・和と差の積の公式

こちらも因数分解で頻出です。応用問題にも利用されます。

・共通な部分を1つの文字におきかえて展開する

応用問題で、たびたび出題されます。また因数分解ではこの展開の逆で、おきかえてから求める方法を用いて解く問題が出題されます。

（３）因数分解

・因数分解とは

多項式を、2つ以上の単項式・多項式の積の形だけで表すことを因数分解といいます。因数分解するには、すでに学んだ「展開」の逆を行います。ある程度、展開後の形を見おぼえていることが重要になります。

因数分解にはおもに以下の方法があります。

２．平方根 

「平方根」という概念を初めて学びます。

（１）平方根

・平方根とは

平方根とは、2乗の逆です。(□)²＝n、つまり同じ数を2回かけ算して任意の数nになるとき、その数(□)をnの平方根といいます。

正負の数があるため、平方根は必ず同じ絶対値で符号が異なる数2つになります。

（例）81の平方根＝±9（＋9と－9）

・平方根の性質

2回同じ数をかけると、たとえ負の数でも正の数になります。同じ数を2回かけて負の数になることはありません（※高校数学では出てきますが中学数学では扱いません）。

よって、負の数の平方根は存在しません。また、0の平方根は0だけです。

・平方根の値と近似値

平方根の値とは、例えば4の平方根は±2です。しかし例えば5の平方根はどうでしょう。2回かけて5になる数字は、正確には求められません。

小数を使って平方根を表すとき、近似値とよばれます。例えば5の正の平方根は、小数で表すと0.22360679…　です。無限小数であり、わりきれないため近似値を用います。

数学の教科書の付録に、平方根の近似値が載っていれば確認してみましょう。ただし覚える必要はなく、おおむねどの程度とわかっていれば大丈夫です。

（２）根号を含む式の計算

・根号とは

5の平方根の値は、小数で表そうとすると無限小数になってしまい、近似値でしか表せません。そこで根号（ルート）という記号を使って表します。

（例）16の平方根＝±√16＝±4

16の平方根は整数になるのでそこまで計算しますが、5の場合は以下のようになります。

（例）5の平方根＝±√5

文字の場合も同じで、xの平方根は±√xとなります。

・根号を含む式の乗法、除法

√どうしのかけ算はルートの数字どうしでできます。

（例）√3×√5＝√3×5＝√15

わり算も同様です。

（例）√26÷√2＝√26÷2＝√13

・根号を含む加法、減法

同じ平方根以外は計算できません。文字式の「同類項をまとめる」のと同じと考えてください。

（例）
√2＋√3　←これ以上計算できない
√5＋2√5＝3√5　←文字式でa＋2a＝3aとなるのと同じ

・ルートの中を簡単にする

素因数分解を利用します。

（例）√24を簡単にする
√24      ＝√2×2×2×3　←ルートの中に2つあるものは整数としてルートの外に出せる
　　　　＝2√6

・分母の有理化

分数の分母に平方根がある場合は、分母を整数にします。これを有理化（有理数にすること）といいます。「分母にかけた数と同じ数を分子にかければ分数の大きさは変わらない」性質を使うため、分母と分子両方に√の数字をかけます。

（例）分母が√7なら、√7を分母と分子両方にかける

（３）平方根の利用

平方根を利用した文章問題が出題されます。

３．二次方程式

2次方程式は1次方程式、連立方程式よりも複雑なため、それぞれの2次方程式に対応する解き方を覚える必要があります。

（１）二次方程式とは

xの2乗の項を含む方程式（xの2次式を含む多項式＝0）を、xについての2次方程式といいます。

（２）二次方程式の解き方

2次方程式の解き方には、以下の3つの方法があります。

（３）二次方程式の解の公式

解の公式とは、2次方程式を一般形にして、その公式にあてはめて解く方法です。因数分解や平方根の考え方で解けないすべての2次方程式がこの公式で解けます。完璧に覚えておく必要がある重要項目です。

【ax²＋bx＋c＝0　の解の公式】　※声に出してとなえて暗記しましょう！

（2aぶんのマイナスbプラスマイナスルートb2乗マイナス4ac）

a、b、cに、それぞれの2次方程式の係数をあてはめて解きます。また一般形になっていない2次方程式は、まず式を移行したりして、一般形に変形してから解の公式を使います。

（４）二次方程式の利用

2次方程式を用いた文章題、応用問題は高校入試でも多く扱われます。さまざまなパターンがあるため、問題演習を何度も繰り返し行い、ある程度の問題の種類を知っておくと解きやすくなります。

2次方程式の文章題も、中1や中2で行った方程式の文章題の解き方と変わりません。何をxで表すかを文章から読み取り、xを使った式で表して、解きます。最後に求めた解が文章題の内容に合っているか（例えば現実の個数などでは、マイナスの解はあてはまらないなど）、そもそも数字は正しいかなどを確認することを忘れずに行いましょう。

４．二次関数

関数は中1で比例と反比例、中2で一次関数を学びました。

2つの変数xとyについて、xの値と対応するyの値がともなって変化しそれぞれ1つに定まるとき、「yはxの関数である」といいます。2次関数では2次方程式の考え方を利用します。

（１）二次関数　y＝ax²

xの2乗に比例する関数の式は以下のように表されます。

（２）y＝ax²のグラフ

・放物線

2乗に比例する関数のグラフは、なめらかなすり鉢状の曲線になります。これを放物線といいます。書くときには表を用いてxとyの値を出し、グラフ上に点をとってつなぎつつ、なめらかな曲線になるように書きます。

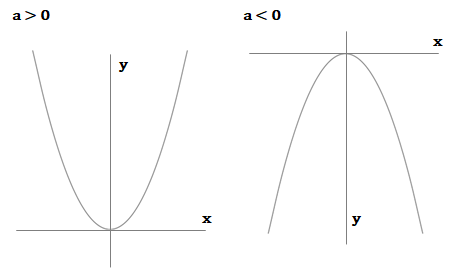
2次関数y＝ax²のグラフには以下の特徴があります。

③の特徴から、y＝ax²のグラフとy＝－ax²のグラフは、x軸について対称の形になります。

・二次関数y＝ax²の値の増減と変域

1次関数ではxの最小と最大の値を代入して求めるyの最小値・最大値（グラフの両端の点）を求めやすかったのですが、2次関数のグラフは原点を通る放物線のため、xの変域がマイナスからプラスにまたがる場合、yの最小値、または最大値は必ず原点（y＝0）となります。

2次関数で変域を考える問題では、少なくとも慣れるまではグラフを書いて確認したほうがよいでしょう。

（３）二次関数y＝ax²の「変化の割合」

1次関数と同じく、2次関数も以下の式で表せます。

（４）二次関数y＝ax²の複合問題など

よく問われるのは、1次関数と2次関数が同じグラフ上に書かれているものです。2つのグラフの交点は2つの式の解になります。

５．図形と相似

中2で学んだ「合同」の発展単元です。

（１）相似な図形とは

・相似の意味

同じ形で大きさの違う図形を相似な図形といいます。

△ABCと△DEFが相似な図形の場合、「∽」を用いて「△ABC∽△DEF」と書きます。

・相似な図形の性質

以下の性質があります。

・相似比とは

上記①の「対応する部分の長さの比」を相似比といいます。

・相似の中心

相似な図形において、

・対応する点どうしを結ぶ直線が1点で交わる
・その1点から、対応する点までの距離の「比」がすべて等しい

という条件がそろうとき、その1点を「相似の中心」といいます。

相似の中心の反対側に相似の図形を書く場合は、図形は180度回転した位置になります。相似の中心から見て同じ側に相似の図形を書く場合は、同じ形のものが同じ方向に書かれます。

（２）三角形の相似条件

三角形の相似条件では辺の「比」が等しくなります。

（３）平行線と線分の比

3本の直線L//M//N（//は平行の意味）のとき、線分の長さはAB：BC＝DE：EFとなる

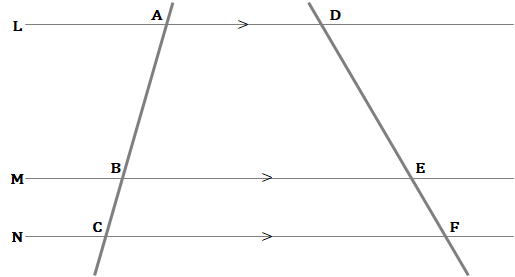
（４）中点連結定理

△ABCにおいて、点M、Nがそれぞれ辺AB、ACの中点のとき、以下が成り立ちます。これを中点連結定理といいます。証明問題で利用します。

・MN//BC

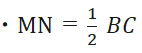
（５）相似な平面の面積比

相似な図形の面積の比は、相似比の2乗の比となります。

（例）相似比がaのとき、面積比はa²

（６）相似な立体の体積比と表面積比

・相似な立体の表面積の比、体積の比

相似な立体の特徴は以下のとおりです。

６．円の性質

円周角の定理を使った問題を扱います。

（１）円周角と中心角

・円周角とは

円周上に点P、A、Bがあるとき、ABを「弧AB」と読む。また∠APBを「弧ABに対する円周角」という。

また、弧ABと中心Oをつないでできる角AOBを「弧ABに対する中心角」という。

・円周角の定理

（２）円周角の定理を用いた問題

いろいろなパターンの問題があり、高校入試では図形問題の大問として扱われます。円と相似を組み合わせたものや体積比、表面積比との複合問題もあり、難易度も平易なものから非常に難解なものまでさまざまです。

また次に学ぶ三平方の定理と組み合わせたものもあります。

対策として、問題演習で数をこなすことが必須となります。

７．三平方の定理

三平方の定理は入試最頻出の単元といえます。ピタゴラスの定理ともいわれ、小学校でも知識として聞いたことはあるかもしれません。これまでの図形問題の例にもれず、問題演習をくりかえし行い、手を動かして実際に自分で図を書いて考えることがポイントです。

（１）三平方の定理とは

・直角三角形の3辺の関係と「三平方の定理」

直角三角形の3つの辺の長さは、以下のような関係が成り立ちます。

a²＋b²＝c²

これを三平方の定理といいます。

直角三角形の3つの辺のうち、最も長い辺は直角の真向かいにあり、これを斜辺といいます。

（２）三平方の定理の問題

三平方の定理を用いた基本の問題は、ある1辺の長さを他の2辺から計算して求めるものです。

ここから、発展問題として以下のような問題があります。いずれも高校入試にも頻出です。

①三平方の定理を使った証明問題
②三平方の定理と円の接線や弦の問題
③グラフにおける座標平面上の2点間の距離を求める問題
④錐体の高さを求める問題
⑤直方体の対角線の長さを求める問題
⑥立体を切断した際にできる図形の面積や、球の切断面を底辺として、中心～球の表面までをつないだ三角形の面積を求める問題
⑦錐体の表面上の糸や線の長さを求める問題

８．標本調査

標本調査は、中1の「資料の整理」、中2の「確率」からつながる単元です。データを集め、全体を推測する力を養います。

以下の2つの用語の理解がポイントになります。

・標本調査：集団の一部を取り出して調査し、集団全体の傾向を推測する
・全数調査：集団のすべてに対して調査

あわせて、母集団の意味や標本の取り出し方、推測の仕方も理解しましょう。

標本調査は、私たちの身の回りから政治経済まで、多くの場面で使われる考え方です。「標本調査の活用」では、具体的な事例を用いて標本調査の考え方を習得します。

(1)できない問題をできるようにする

中3の時間は限られています。時間をできるだけ有効に活用するために、できない問題をできるようにする学習を意識しましょう。

たとえば「55-23」「23×5」などの基本的な四則演算は、毎日わざわざ練習しなくてもサラッと解けませんか？解き方が身体に染みついているからです。

同じように、中学の数学でもわざわざ練習しなくても解ける単元があるはずです。

しかし日々の学習では「なんとなく」「惰性で」「考える問題は面倒だから」と、できる問題を練習して勉強した気になってはいないでしょうか。それはもったいない時間の使い方です。

成績は「できない問題をできるようにする」ことでしか上がりません。できない問題に取り組むのは億劫かもしれませんが、覚悟を決めて取り掛かってみましょう。

(2)「解答の方針立て」に頭を使うようにする

中3数学における「できない問題」は、推論が必要な問題であるケースが多いようです。解くために手を動かす前に解答の方針を立てなければならず、しかしなかなか方針が立たずあきらめてしまう中学生が大勢います。

冒頭で解説したように、推論が必要な問題が増えるのは中3数学の特徴です。高校数学で必要な力の土台を中3から鍛え始めようとしている、ともいえるでしょう。

「中3の数学は思考に頭をつかうもの」ととらえ、面倒がらずに試行錯誤する勉強を大切にしてください。

ノートに何度も「こうかな？」「いや、この方法かな？」と書きまくった思考プロセスは、一つひとつかならず実力になっていきます。

(3)他都道府県の入試過去問にもチャレンジする

学習指導要領の改訂以降、高校入試で出題される問題に変化が起きています。問題文の長文化により読解力が必要になった問題や、複数の単元を融合させた新傾向の問題などが該当します。

新しいタイプの問題は、いままさに生まれつつある最中です。出題する側も最適な問題を模索している最中のため、お子さんの入試で突然新しい問題がでる可能性もあります。

中3数学の入試対策では、全国各地の高校入試問題にも取り組みましょう。各都道府県が新しい学習指導要領に合わせて問題を作っているため、新傾向の問題に数多く取り組めます。

これまで高校入試対策といえば、お住まいの都道府県の傾向に合わせるのがセオリーでした。しかし、現在では「5年前の自県の問題より、直近1～2年の他県問題のほうが効果的」になりつつあります。

全国の高校入試問題を収録した「全国高校入試問題集」も市販されています。ぜひチェックしてみてください。

数学を学ぶメリット

数学は、「なぜ学ぶのか」という疑問を抱かれやすい教科です。抽象的で論理ばかり追い求める数学の特性が、そう感じさせるのでしょう。実学（実生活で役立つ学問）とも言い難い側面も、影響しているのかもしれません。

しかし、数学を一生懸命学ぶことで得られるメリットは、計り知れないものがあります。数学を通じて得られるメリットを紹介します。

(1) 論理的に考える力が育つ

数学は、論理の学問です。どのような問題にもかならず前提条件があり、その条件を踏まえた上で順序だてて考えなければなりません。解き方に無理があったり、筋道が通っていなかったりすると、すぐに指摘されます。

「なぜそうなるのか」を、これほどまでに深く追求する学問はないでしょう。この「なぜそうなるのか」を突き詰める力こそが、論理的思考力です。数学が得意になると、物事を順序だてて考えられるようになり、生産性や効率がアップします。

(2) 表現力が身につく

文章題や証明問題に取り組むと、途中過程もしっかりチェックされます。時には、導出した解が正解値でも、途中の考え方や書き方が間違っていたために、不正解とされるケースもあります。

これは、数学が論理を大切にする学問だからこそ見られる特徴です。論理が通るように物事を考え、その考えと論理が正しく相手に伝わるよう、誤解や矛盾のない表現で書き切る必要がある学問なのです。

数学を学ぶ中で、相手との齟齬のないコミュニケーションを成立させるスキルを伸ばすこともできるでしょう。

(3) 問題発見力・問題解決力が養われる

数学は、学んだ内容を新しいパターンの問題に応用したり、初めて見る問題に挑戦し試行錯誤したりする場面が多い教科です。自分が知っている知識や持つノウハウを使って、初見の問題に挑む姿勢は、問題発見力や問題解決力を養成します。

何をヒントに手がかりを見つければ良いのか、そのヒントをどのように活用するのかなど、問題を解く過程の一つひとつに、問題発見力・問題解決力を伸ばすポイントが隠されています。

問題発見力・問題解決力は、一生涯役立つスキルです。ぜひ、数学で存分に伸ばしていってください。

数学が面白くなる雑学

数学に関する雑学を、少しだけ紹介しましょう。「そうなんだ！」と感心するものがあったら、ぜひ自分でも調べてみてください。数学への興味の扉を開くきっかけになってくれるかもしれませんよ。

(1)三平方の定理の証明は100通り以上ある

中3の最後に習う三平方の定理は、古代ギリシアの数学者・ピタゴラスが発見しました。三平方の定理は、その美しさやシンプルさで、またたくまに、数学界の人気公式となります。

そして、この公式を証明しようと、多くの人が挑戦しました。その結果、数百通り以上もの証明法が見つかったといわれています。

1つの公式の証明が数百通り！当時にテストがあったら、どの証明法を書くべきか悩んでしまいそうです。

(2) 角の3等分線は作図できない

私たちは数学で、角の2等分線を作図する方法を学びました。ところが、3等分線となると作図できないのだそうです。

角の3等分線自体は、存在します。角度を分度器で測って3等分し、その線を引けば良いのですから。ところが、このやり方は定規とコンパスで書いてはいませんから、作図とはいえません。

角の3等分線が作図できないことは、フランス人数学者ピエール・ローラン・ヴァンツェルによって、1837年に示されています。

(3) 解の公式は4次までしかない

2次方程式で登場する解の公式は、覚えるのに苦労する公式の1つです。

さて、2次方程式に解の公式があるなら、3次方程式にもあるのでしょうか？答えは「ある」です。そして、4次方程式にも、解の公式が存在します。

ただ、3次と4次の解の公式は、高校数学の範疇も逸脱する、とても複雑な式。ゆえに、ここでは割愛します。

では、5次方程式の解はあるのか。

答えは「ありません」。5次にも6次にも、7次にも…、その先ずっと、解の公式は存在しないそうです。5次方程式以上に解の公式がないことは、アーベル-ルフィニの定理という理論で証明されています。

中学3年生の数学習得におすすめの塾5選

中学3年生になると、いよいよ高校受験までのカウントダウンが始まります。残り時間が限られる中、効率良く数学対策を進める方法はあるでしょうか。

解決策の1つが、塾の利用です。一人ひとりに合ったペースで授業が進む個別指導塾なら、苦手単元の克服にも受験に向けた演習も、フル活用できます。

ここからは、数ある個別指導塾の中でも、塾探しの窓口編集部が自信をもっておすすめする塾を5つ紹介します。

個別教室のトライ

個別教室のトライは、全国に約650教室を展開する大手個別指導塾です。すべての教室・すべての授業が、完全マンツーマン。授業中、講師は生徒につきっきりになり、数学の解き方や考え方、推論の取り掛かりポイントまで指導します。

個別教室のトライでは、仕切られた専用個別ブースで授業をします。周りの目を気にせず、自分がいまやるべき問題に没頭できる環境で、集中力やじっくり考える力が育ちます。

同時に、過去140万人の指導実績から生まれた「トライ式学習法」も教えてもらえます。暗記法や復習の仕方など、全教科の受験勉強に役立つ方法ばかりです。

お近くに個別教室のトライがない場合は、トライのオンライン個別指導塾をご検討ください。自宅にいながら、トライ品質の授業を受けられるオンライン指導サービスです。

個別教室のトライの料金情報は、以下のとおりです。

東京個別指導学院・関西個別指導学院

東京個別指導学院・関西個別指導学院は、講師1人に生徒が2人つく個別指導塾です。講師が解説する時間は1対1となり、他の生徒を指導する時間は演習に取り組みます。解説を聞いて理解し、演習で定着させるという学習サイクルが確立されており、理想的なペースで数学を学んでいけます。

一人ひとりに合わせて計画を立て授業を進めるため、「受験に間に合わせたい」「次のテストで結果を出したい」など、どのような目標にも対応可能。学校進度と復習の同時進行もでき、中3の数学を効率良く習得できます。

教育大手・ベネッセのグループ塾として、受験情報にも精通。東京個別指導学院・関西個別指導学院に通うだけで、必要な情報を随時入手できます。

東京個別指導学院・関西個別指導学院の料金情報は、以下のとおりです。

個別指導WAM

個別指導WAMは学校に合わせた対策や、受験対策に定評ある塾です。中3生の数学定期テストに合わせて、新出単元と既習単元を網羅した計画を策定。必要な学習を、無理なくマスターしていけます。

学習プログラムの策定にAIを活用するのも、個別指導WAMの特徴です。人の目では見つからない、細かな苦手や課題をも漏らさずピックアップし、数学全体の底上げを図ります。

定期テストや単元テストで着実に結果を残せるため、内申点の向上も期待できるでしょう。

お近くに個別指導WAMの教室がない場合は、自宅で受講できるオンライン家庭教師WAMを活用しましょう。対面指導と遜色ない品質の授業を、リーズナブルな費用で受けられます。

個別指導WAMの料金情報は、以下のとおりです。

※ 返金制度あり

代々木個別指導学院

代々木個別指導学院は、めんどうみのよい講師が教科指導から勉強のやり方まで、親身に寄り添い指導する塾です。生徒一人ひとりに完全に合わせて作成する「キミ専用カリキュラム」で、いまやるべき学習内容を明確化。褒めて励ますスキルを持った講師が、共に目標達成まで伴走します。

自分のペースで進められる「フリーステップ学習」や、わかるまで繰り返す「反復学習システム」など、成績アップを実現する独自の学習メソッドも豊富。教えすぎず、生徒自身の頭で考える時間を重視する指導スタイルで、自主的に取り組む姿勢が育まれます。

公立高校受験はもちろん、私立高校や一貫校生の内部進学対策にも対応しています。

代々木個別指導学院の料金情報は、以下のとおりです。

ナビ個別指導学院

「学校の授業を聞いても、よく理解できない」、そんな中3生にはナビ個別指導学院がおすすめです。ナビ個別指導学院は、濃密な解説授業を得意とする塾。わからない問題を教えるだけでなく、そもそもの考え方や解き方から理解し、自分で考え導く力を養います。

授業を担当する講師と教室長とが、二人三脚で生徒にかかわる頼もしい面もあります。複数の視点で分析することで、精度高く、生徒により適した授業が可能になるのです。

一般的な塾の体験授業は1～2回のところ、ナビ個別指導学院の体験授業はたっぷり4回分。「通塾」を体験し、納得してから始められる、嬉しいシステムを試してみてはいかがでしょうか。

ナビ個別指導学院の料金情報は、以下のとおりです。

まとめ

中3数学で習う単元の内容についてポイントを解説しました。

中3数学は高校の数学につながる重要な内容ばかりです。また中学で学んだすべての内容をふまえた複合問題が増えています。そのため、わからないところが出てきたら、中1や中2の内容まで戻って復習する必要があります。高校受験が控えている場合は、不明点をできるだけ早く（中3になる前の春休みまでに）チェックしてつぶしておきましょう。

数学が苦手な生徒さんが一人で復習や弱点克服を進めるには、中3数学は難しいため、苦手意識ができる前に早めに塾などを利用し、対策することをおすすめします。

「塾探しの窓口」を使うとお子様の学習状況、性格やスケジュールに合った塾がエリアごとに探せます。上手に利用してお子様の数学の学習にお役立てください。

【中学生】数学に定評あるおすすめ塾17選｜選び方も解説

中学生に苦手教科を尋ねると、筆頭に挙げられるのが数学です。さまざまな調査でも、数学は「苦手教科ナンバーワン」の不名誉…

詳しく読む

【中学生向け】おすすめの個別指導塾17選！編集部が厳選

定期テストの点数を見て「うちもそろそろ塾が必要かな？」とお悩みでしょうか。高校受験に向けて勉強して欲しいと思う一方で、…

詳しく読む

【高校受験】勉強はいつから始めれば間に合う？元教員が解説

お子さんが高校受験を控え、 ・一般的に受験勉強を始める時期はいつ頃が多いのか・受験勉強は、間に合う（＝合格する）た…

詳しく読む