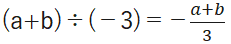学習塾の口コミ比較サイト「塾探しの窓口」が運営。初めて塾を探されている保護者に向けて、塾を探す上での基礎知識や塾選びを成功に導くためのポイント等を、わかりやすくお届けします。
【数学】中1で習う単元をまとめて要点解説 | 習得したい勉強のコツも紹介

中学生になって、算数から数学に変わったことで戸惑う人もいるのではないでしょうか。
中1は、数学の基礎を学ぶ学年です。中1数学で学ぶ内容と中1数学が重要な理由、押さえておきたいポイントについて解説します。
中1で習う数学の概要

中1では、小学校までの算数が「数学」になります。高校まで続く数学の始まりです。
算数が数学になると、扱う情報の抽象度が上がります。算数では、買い物やおやつの分け方など日常の具体的な計算を学んできました。一方数学になると「x、y」などの記号を使い机上の論理を学ぶようになります。
また数学では単に答えがでれば良しとはされず、答えに至るまでの考え方(いわゆる「論理的思考力」)も重視されるようになります。数学は「答えは○○となる、なぜなら△△という理由だから」と明解に説明できる力も必要な教科です。
中1の数学は新しい内容の学習内容と、「具体から抽象へ」「解答から思考過程へ」という教科の性質そのものの変化を同時に習得する必要があります。
教科の性質変化についていけないと「小学校までは算数が得意だったのに、中学に入った途端数学が苦手になった」となりかねません。
学習内容をしっかり理解するのと同時に、抽象概念の扱い方や論理的に考える力も意識して学んでいきましょう。
中1数学を勉強する際の注意点

数学の学習をスタートするにあたり、押さえておきたい注意点を解説します。最初でつまずかないよう、一つひとつチェックしていきましょう。
(1) 自問し、納得する姿勢を大切にする
中1の数学を勉強する際は、「つまりどういうことか」と自問する意識を持ち続けましょう。
中1数学の関門である「情報の抽象化」は、中1の最初からいきなり始まります。また学習が進むにつれ、抽象度は徐々に上がっていきます。
学習内容を本質的に理解していないと、自覚のない「わからない」がどんどんつみ重なってしまいます。
理解不足を自覚したころには手遅れになる恐れもあるため、単元一つひとつを「つまりどういうことか」と考えながら学び、深く理解するよう心がけてください。
(2) 自問する学びの具体例
「つまりどういうことか」と考えながら学び、深く理解するとは、具体的にどのような姿勢を意味するのでしょうか。具体例を挙げながら、見てみましょう。
中1数学の2番目には「文字の式」という単元が登場します。続く3番目には、よく似た「方程式」が続きます。両者の問題を、以下に並べました。見比べてみてください。
| 「文字の式」の計算問題(例) | 方程式の計算問題(例) |
| 問、次の計算をしなさい。 (6x+5)+(7x−13) | 問、次の計算をしなさい。 6(1-x)=-x+11 |
ちなみに正解は以下のとおりです。
・文字の式 13x-8
・方程式 x=-1
文字の式は同じ文字の項目や数字をまとめ、もっともシンプルな形にする計算です。一方方程式は(左辺)=(右辺)を成立させるxの値を求める計算です。
この本質を押さえず、「文字の式は解答に=がない」「方程式はx=〇の形で答える」と、形式的な理解だけで式を操作すると、以降の単元でかならずつまずきます。
中1数学では「つまりどういうことか」と自問しながら、本質から理解する姿勢を大切にしましょう。
1.正の数・負の数
ここからは、中1数学で習う単元とその内容を、簡単に解説します。まずは、正の数・負の数から始めましょう。
(1)数の大小・数直線と絶対値
・数の大小
小学校でまでで学んできた数は、正の数です。数直線では、0より右側に表されます。そして、中学数学では数直線の0から左側に置かれる「負の数」が登場します。
正の数は「+150」のように「プラス」をつけて表すこともありますが、一般的にプラスの符号は省略します。負の数は「-150」のように、数字の前に「-(マイナス)」記号をつけます。この-は省略できません。
数の大小は不等号(<,>)で表します。
(例)-150<1.5
・数直線と絶対値
数は、数直線の右側に行くほど大きく、左側に行くほど小さくなります。見た目の数字が大きくても、この原則は変わりません。小数や分数でも同じです。
「見た目の数字」を絶対値といいます。絶対値は「数直線上の0からの距離」です。150も-150も、絶対値は150です。
(2)正の数と負の数の加減乗除
・正の数と負の数の加法、減法(足し算と引き算)
小学校では正の数どうしの足し算と引き算だけでした。中学では正の数と負の数の足し算と引き算を学びます。
基本の考え方は、0を起点に、「+ならば右へ移動」「-ならば左へ移動」です。初めは数直線を引いて考えましょう。当たり前のように計算できる状態になるまで、繰り返して練習することが大切です。
・正の数と負の数の乗法、除法(かけ算とわり算)
正の数・負の数の掛け算と割り算では、とくに負の数をかける(かけられる)場合に注意してください。負の数をかける(かけられる)と、答えはかけられる(かける)数の符号と逆になります。★は特に間違えやすいので何度も解いて覚えましょう。
・正×正=正
・正×負=負
・負×正=負
・負×負=正★
この符号のルールは、わり算でも同じです。
・正÷正=正
・正÷負=負
・負÷正=負
・負÷負=正★
3. 方程式
(1)方程式とは
先に習った文字式と似ていますが、しっかり区別しなければならないのが方程式です。方程式とは、イコールで結ばれた左右の式が、特定の値を代入した際に成り立つ式を指します。
イコールの左側を「左辺」、右側を「右辺」といいます。
(例)
x-3=5
→ この式はx=8のときに左右とも5となり、成立する(方程式)
x+10=3x-2
→ この式はx=6のとき左右とも16となり、成立する(方程式)
なお、中1では未知の数(x)が1つだけの方程式を扱います。未知の数がx、yと2つ以上ある場合は連立方程式と呼ばれる方法で解く必要があり、こちらは中2で登場します。
(2)方程式の解き方
方程式は、両辺にある項を整理しながら解きます。原則的に、文字の項は左辺に、数字の項は右辺に集めてください。
イコールをまたいで項を移動させる際、項の符号を変えます。
(例)
x-3=5
└ 左辺の-3を右辺に集める(数字は右辺)
x=5+3
└ -3がイコールをまたいで移動したため、符号がプラスに変わる
右辺を計算して、x=8
イコールをまたいで項を移動させる作業を「移項」といいます。
(3)方程式の利用
方程式の単元では、多くの文章題が登場します。典型的な問題を1題、みてみましょう。
(例題)
折り紙を何人かの子どもに配る。1人に8枚ずつ配ると8枚あまり、10枚ずつ配ると6枚足りない。子どもの人数と折り紙の枚数をそれぞれ求めなさい。
(解き方)
未知の数は、子どもの人数です。これをxとします。
◎ 1人に8枚ずつ配ると8枚あまる→ 8x+8
◎ 1人に10枚ずつ配ると6枚足りない→ 10x-6
8x+8、10x-6ともに、ここにある折り紙の数を示しているわけですから、
8x+8=10x-6
-2x=-14
x=7
従って、子どもの人数は7人
折り紙の枚数は8x+8、10x-6のいずれかにx=7を代入して
折り紙の枚数は64枚
方程式の利用は、提示された条件を丁寧に見比べ、論理的・段階的に考える力が養成されます。中2数学に直結する単元、かつ高校入試で頻出の単元でもあるため、しっかり練習しておきましょう。
(7)比例と反比例の利用(文章題など)
演習問題を解いて練習しましょう。
5.平面図形
(1)直線と図形
・直線、線分、半直線の意味
まっすぐに限りなく伸びる線を「直線」といいます。2つの点を通る直線は1本だけです。点Aと点Bを通る直線を「直線AB」と呼びます。また片側だけに無限に伸ばしたものを「半直線AB」といいます。
直線も半直線も無限ですが、AからBまでで切り取られた部分を「線分AB」とよびます。
線分を二等分する点を「中点」といいます。また直線に垂直に交わる直線を「垂線」といいます。
線分の中点を通る、その線分に垂直な直線を「垂直二等分線」といいます。
・角の表し方
角は、∠の記号を使って表します。2本の半直線OA、OBではさまれた間を∠AOBと表します。
・垂直な2直線、平行な2直線の意味と表し方
垂直な2直線はAB⊥CD、並行な2直線はAB//CDと書きます。
・三角形の表し方
三角形は頂点を続けて読んで、「三角形ABC」といいます。△ABCと表します。
(2)空間における平面と直線
空間内における平面や直線の位置関係と、平面が一つに確定する条件などを学びます。
・平面が一つに決定する条件
①1直線上に無い3点があるとき
②直線と1点があるとき
③平行な2直線があるとき
④交わる2つの直線があるとき
・空間内の2直線の位置関係
空間内の2つの直線の位置関係には「交わる」「平行」「ねじれの位置」の3つがあります。
上の「平面が一つに決定する」条件のとおり、「交わる」と「平行」の場合は、同じ一つの平面上にあることになります。
また同一平面上になく、交わりもしていないものは「ねじれ」の位置関係となります。
・空間内の直線と平面の位置関係
「平行」「交わる」「平面上にある」の3つになります。
・空間内の2つの平面の位置関係
「平行」または「交わる」の2つになります。
中1数学が重要な理由

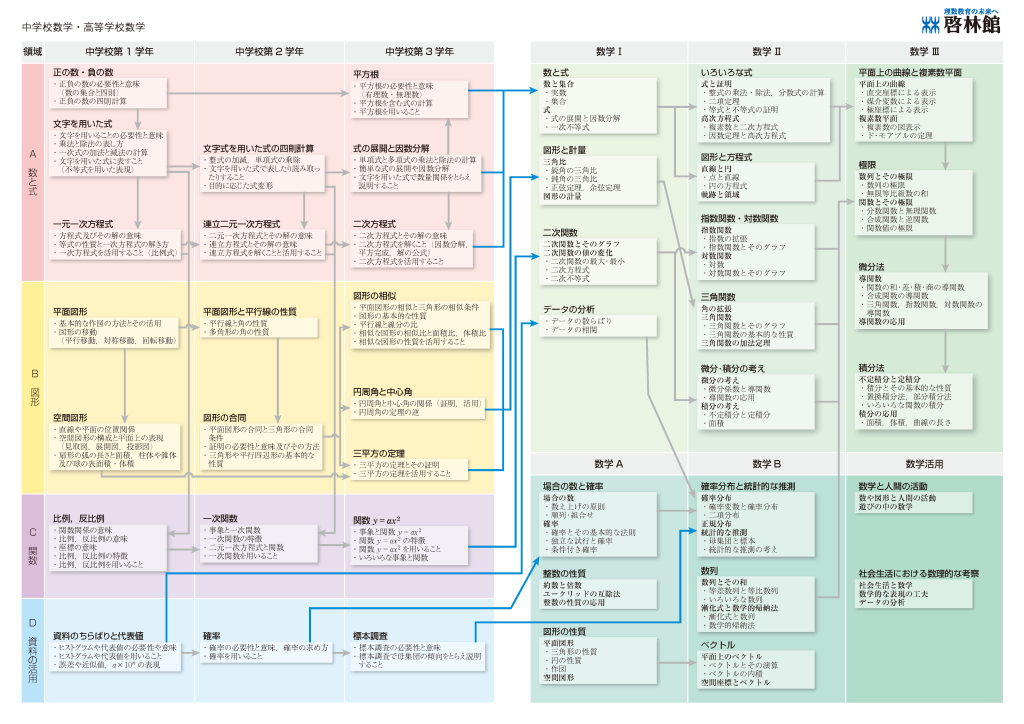
「中1数学は大切だ」と、学校の先生も繰り返し言うのではないでしょうか。なぜ、中1数学が大切なのか。その理由は、下の図を見るとわかります。
※ 新学習指導要領における算数・数学内容系統一覧表|啓林館
この図は、教科書会社が作成した、数学の単元同士のつながりを可視化したものです。一番左に中1数学があり、右に進むにしたがって学年が上がります。矢印は、単元同士の関連性があることを示します。
どうでしょうか。中1数学は、すべての単元が中2以降につながってはいないでしょうか。
中1で学ぶ方程式は、中2の連立方程式、中3の二次方程式につながります。また、中1の比例・反比例は中2で一次関数、中3で二次関数となっていきます。当然、高校では中学数学を習得しているものとして、高校数学の授業が進みます。
中1で数学につまずくと、以降の単元内容の理解が非常に難しくなります。苦手を克服しようと思ったら、受験生であっても中1の内容までさかのぼらなければなりません。
中1数学は、学校に通う限り続く数学の礎となる、とても大切な教科です。一つひとつの事項を丁寧に、時間をかけて理解し、復習しながら身につける努力を続けましょう。
自力での学習が難しい場合は、早めに塾のサポートを頼ることをおすすめします。
中1数学 勉強のコツ

中1の数学は「いま、自分は何の作業をしているのか」を考えながら解く学習が効果的です。高校入試、その先の高校数学まで使える数学学習のコツを3つ、解説します。
(1)計算は「考えなくても手が動く」レベルを目指す
「つまりどういうことか」と本質を理解したら、演習により単元の完全習得を目指します。計算は考えなくても手が動くレベルを目指し、反復学習に取り組んでください。
定期テストや高校入試において、数学は「時間との勝負」になりやすい教科です。第1問で出される計算に手こずっていては、高得点獲得は見込めません。またどの単元を学ぶにせよ、計算は数学の基本となる力です。
数式を見た瞬間に手が動きだし、正解を導ける完成度を目指し、トレーニングしていきましょう。
(2)練習する問題は例題・練習問題レベルから徐々に上げる
「テストで配点が高い応用問題こそ得点すべき」といきなり難しい問題から始めると、お子さんを数学嫌いにする原因になります。まずはお子さんが自信を持って正解できる、教科書例題レベルから始めましょう。その後、定期テストに向けて章末問題、応用問題…と、取り組む問題バリエーションを増やします。
例題・練習問題は、「いまどのような処理をしているのか」「解答までの道のりの何合目くらいにいるか」など、お子さんが問題を解きながら自分を客観視する余裕が持てる点もメリットです。
(3)毎日勉強する習慣を身につける
生活リズムが小学生までとはガラリと変わる中1は、勉強の習慣づけをしやすいタイミングでもあります。数学の宿題や自主学習を利用し、毎日勉強する習慣をつけておきましょう。
数学は、1日サボると知識の定着度が大きく下がる教科ともいわれます。とりわけ計算のスピード・主熟度は繰り返しと継続がつくるため、できるだけ毎日取り組むようにしてください。
「帰宅してすぐ」「夕食後」など机に向かいやすいタイミングを決め、勉強に促すのも良い方法です。
中1数学を得意教科にできる!おすすめの塾5選

単元を一つひとつ積み上げながら理解する数学は、わからない単元を放置すると、あっというまに数学全体が苦手になってしまいます。反対に、早いうちから対策をはじめ、順を追って丁寧に理解していけば、得意教科・得点できる教科に育てることも可能です。
論理的な思考や分析の力も必要になる数学対策は、塾の利用がおすすめ。ここからは塾探しの窓口の編集部が厳選した数学対策におすすめの塾を5選紹介します。
個別教室のトライ
個別教室のトライは、完全マンツーマン授業を提供する塾です。生徒1人に講師1人が付きっきりになり、仕切られた個別ブースでじっくりと数学に向き合えます。授業のペースやレベル、構成を自由に決められるのは、マンツーマンならではの魅力。苦手な単元は時間をかけて、得意な単元はハイレベルな演習を、と授業内容の柔軟なカスタマイズも可能です。
個別教室のトライ全教室には、開校時間中は自由に使える自習室も完備。数学の宿題やテスト勉強、受験勉強にと活用できます。
お近くに個別教室のトライがない方は、オンラインで受講できるトライのオンライン個別指導塾はいかがでしょうか。トライ品質の授業を、対面指導よりリーズナブルに受けられます。
個別教室のトライの料金情報は、以下のとおりです。
| 入会金 | 11,000円 |
| 授業料(目安) | 中学生 26,000円~30,000円/月 |
| その他の費用 | 季節講習あり(中学生は35,000円~70,000円程度) ※ 教材費は不要 |
無料資料請求する
東京個別指導学院・関西個別指導学院
「部活が忙しいが、数学も頑張りたい」、そんな中学生には東京個別指導学院・関西個別指導学院をおすすめします。東京個別指導学院・関西個別指導学院は、細やかな指導と人間力にあふれた講師、そして柔軟な対応力に定評ある塾です。
東京個別指導学院・関西個別指導学院では、生徒と講師の相性を大切にしています。学力や人間性などの厳しい審査を突破した講師は、研修を受けてから授業を担当。また、生徒との相性を確認するために、本格的な授業開始前には複数の講師と体験授業を実施するという徹底ぶりです。
授業の欠席連絡は、当日の授業開始前までOK。別の日に無料で振替授業を実施します。部活の練習が長引いても、試合や大会が入っても安心して両立できる、嬉しいシステムです。
東京個別指導学院・関西個別指導学院の料金情報は、以下のとおりです。
| 入会金 | なし |
| 授業料 | 受講教科や回数、ペース、使用教材などによって変動 要問合せ |
| その他の費用 | 季節講習あり |
無料資料請求する 最短1分で完了! 関西個別指導学院のお近くの教室に
無料資料請求する
個別指導WAM
個別指導WAMは、教室がある地域の中学校に合わせて授業を構成します。学校の進度やテスト範囲にピッタリ合わせられるため、学校と塾の学習が相乗効果を発揮。理解と定着が効率良く進み、数学を深く、正しく習得していけるでしょう。
難関大生やプロ講師を中心とした、実力派講師陣も注目ポイントです。数学のつまずきやすい要点を熟知した講師が、苦手になる前に問題を解消。「わかる」「できる」実感を育てます。
自宅でWAMの授業を受けられるオンライン家庭教師WAMも、人気のサービスです。周りを気にせず、自分のペースで集中したい中学生は、オンライン家庭教師を検討してみても良いでしょう。
個別指導WAMの料金情報は、以下のとおりです。
| 入会金 | 入会金と登録料が必要、金額は要問合せ |
| 授業料 | 中1・2→7,600円~ 中3→8,400円~ ※週1回・40分コースの月額 |
| その他の費用 | 年会費 維持管理費(毎月) e-ラーニング教材費 |
※ 返金制度あり
最短1分で完了! 個別指導WAMのお近くの教室に無料資料請求する
代々木個別指導学院
代々木個別指導学院は、めんどうみの良い講師が、わかるまで徹底的に指導する塾です。授業は、通う中学と現状、目標にピッタリの「キミ専用カリキュラム」で策定。学年をさかのぼっての復習や、生徒の理解に合わせたペースでの授業など、本当にわかるようになるための工夫が満載です。
生徒が自分で考え、取り組む主体性を大切にするのも、代々木個別指導学院スタイル。講師は手取り足取り教えず、生徒が自分の頭で思考する時間を尊重します。
自分でやるから、本当にできる。そんな実感を抱けるようになる塾、それが代々木個別指導学院です。
代々木個別指導学院の料金情報は、以下のとおりです。
| 入会金 | 20,000円 |
| 授業料 | 10,800円~/1科目 |
| その他の費用 | 季節講習あり(30,000円~40,000円程度) |
無料資料請求する
ナビ個別指導学院
「数学が好き」「数学が得意」となるためには、まず数学の楽しさを知らなければなりません。ナビ個別指導学院は、親身に寄り添ってたくさん褒める講師がいる塾。小さな努力もすかさず認めてもらえるため、生徒のやる気が生まれ、やがて数学と勉強を好きになるサイクルが生まれます。
「やればできる」という自信を確実に育む自信は、成績アップ保証の実施に表れています。ナビ個別指導学院の成績アップ保証は、規定を達成できなければ、翌学期3ヶ月分の授業料が免除されるという仕組みです。
まずは4回分が無料で受けられる体験授業で、ナビ個別指導学院の指導を見てみてはいかがでしょうか。
ナビ個別指導学院の料金情報は、以下のとおりです。
| 入会金 | 22,000円 |
| 授業料 | 中1・2→12,600円 中3→16,800円 ※ 週1回授業を受けた場合の月額 |
| その他の費用 | 諸経費 3,480円/月 季節講習あり(コマ単価3,700円~3,800円) |
無料資料請求する
まとめ
中1数学で習う単元の内容について解説しました。
中1の数学は入口であり、今後の学びにとって非常に重要です。難しいと感じたら、苦手意識ができる前に早めに塾などを利用し、対策することをおすすめします。
「塾探しの窓口」を使うとお子様の学習状況、性格やスケジュールに合った塾がエリアごとに探せます。上手に利用してお子様の数学の学習にお役立てください。



中学生向けのおすすめ塾
中学生向けの塾の料金・口コミ
- 個別教室のトライの料金・口コミ
- 東京個別指導学院・関西個別指導学院の料金・口コミ
- 代々木個別指導学院の料金・口コミ
- 個別指導WAMの料金・口コミ
- ナビ個別指導学院の料金・口コミ
- 中高一貫校専門 個別指導塾WAYSの料金・口コミ
- スタディコーチの料金・口コミ
- 坪田塾の料金・口コミ
- 個別指導塾トライプラスの料金・口コミ
- 個別指導学院サクシードの料金・口コミ
- 個別指導スクールIEの料金・口コミ
- 個別指導塾スタンダードの料金・口コミ
- 個別指導塾サクラサクセスの料金・口コミ
- ドリームホームスクールの料金・口コミ
- みやび個別指導学院の料金・口コミ
- ITTO個別指導学院の料金・口コミ
- コノ塾の料金・口コミ
- 学習空間の料金・口コミ
- キズキ共育塾の料金・口コミ
- 森塾の料金・口コミ
- 自立学習REDの料金・口コミ