学習塾の口コミ比較サイト「塾探しの窓口」が運営。初めて塾を探されている保護者に向けて、塾を探す上での基礎知識や塾選びを成功に導くためのポイント等を、わかりやすくお届けします。
【中1数学】反比例の重要ポイントと解くコツをわかりやすく解説

反比例は「なんとなくわからない」とよく言われる単元です。授業中も先生の解説を聞き、表やグラフを書くので精いっぱい、とても理解まで追いつけなかった人も多いのではないでしょうか。
また比例に比べて授業時間が短く、その後も登場する気配がないため、反比例は関数分野のなかでも軽視されがちです。
ところが反比例は関数全体にかかわる「考え方」の理解に重要な役割を果たします。反比例がわからなかったために、中2や中3で苦労する中学生も少なくないのです。
この記事では中1で習う反比例を、「そもそも反比例とは?」という基本から丁寧に解説します。典型的な問題を使いながら、解き方・考え方もまとめました。
反比例をマスターし、中学関数分野を得意にする足がかりをつかむヒントにしてください。
「反比例」とは

反比例とは「ともなって変わる2つの数のうち、片方が2倍、3倍…となると、もう一方は1/2倍、1/3倍…となる関数」です。
小学校の復習も兼ねて、反比例の全体像を振り返ってみましょう。
(1) <復習>小学校で学んだ比例・反比例
小学校の算数では、「2つの量の変わり方」の単元で比例について小学5年生で学び、比例・反比例としては小学校6年生で学習しました。
ともなって変わる2つの数x、yについて、xが2倍、3倍…になると、yも同じように2倍、3倍になるのが「比例」です。
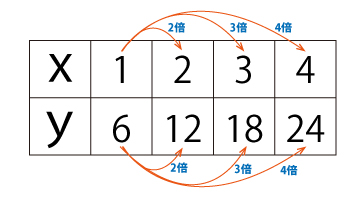
上の表はxが2倍、3倍…になるにしたがってyも2倍、3倍…となっています。そのため「比例の関係にある」といえ、式はy=6xで表されます。
一方が増えると、もう一方も一定の割合で増えていくのが「比例」ですね。では反比例はどのように勉強したでしょうか?
反比例は片方が2倍、3倍…となると、もう一方は1/2倍、1/3倍…となります。表にすると、次のようになります。
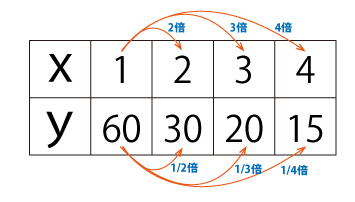
表ではxが2倍、3倍…と増えていますが、yは1/2、1/3…と減少しています。このように片方が増えると、一定の割合でもう一方が減る関係にある関数を「反比例」といいます。
上の表の反比例は、y=60/xと表されます。
反比例の式やグラフについては、次の章で詳しく学習します。ここでは「2つの数について、一方が2倍、3倍…となると、もう一方が1/2倍、1/3倍…と変わる関係を反比例という」を押さえておきましょう。
「100個のチョコレートを、何人かで均等に分ける」シーンをイメージしてみましょう。チョコレートの数は100個と決まっています。分ける人数が5人なら1人あたり20個、10人なら1人あたり10個…となりますね。
つまりチョコレートを分ける人数(x)が2倍になると、もらえる数は1/2に減ります。これが反比例です。「1人あたりのチョコレートの数は、人数に反比例する」といいます。
反比例は私たちの生活のさまざまな場面に登場します。いろいろと探してみてください。
(2) 中学校で学ぶ反比例とは
中学校で学ぶ反比例も、基本の考え方は小学校と同様です。
ただし中学生らしく「負の数」が登場する点を押さえておきましょう。
「y=-12//x」「y=-5/x」といった式も扱います。表やグラフをつくる際も、負の数の存在を忘れないことが大切です。
反比例の基本を理解しよう

いよいよ、中学の反比例を具体的に学習していきます。中学の反比例で確実に押さえておきたいのは、反比例の式の計算とグラフの書き方です。
1つずつ、丁寧に考えていきましょう。
(1) 反比例の式
反比例の式は、次のように表わします。
※ aは「比例定数」
比例定数とは、xとyの関係を表す定数(決まった値)です。比例でも登場しましたね。
y=3xという比例の式では3が比例定数です。yは常にxの3倍の値をとることを意味します。
たとえば、次のような表について考えてみましょう。
| x | 1 | 2 | 3 | 4 | 6 | … | 12 |
| y | 12 | 6 | 4 | 3 | 2 | … | 1 |
xが増えるにしたがってyは減少しており、これは反比例です。
式は
y=12/x
です。
ちなみにこの反比例の式は、変形すると
xy=12
となりますね。
実際に問題を解く場面では、xy=aとしたほうが考えやすいケースも多々あります。どちらでも使いこなせるようにしておきましょう。
(2) 反比例のグラフ
反比例のグラフをかく問題は、定期テストでもよく出されます。値を確実にとり、正しく書けるよう練習しましょう。
反比例のグラフは、次のような形になります。
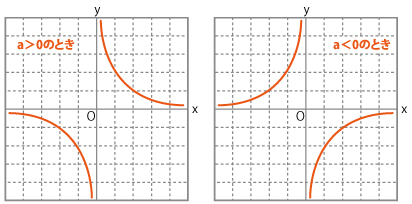
2.反比例のグラフは双曲線状になります。
3.x軸、y軸付近は限りなくx、y軸に近づくようにかきます(漸近線)。
双曲線とは、2つの定点からの距離の差が一定であるような点をつなげた線です。また漸近線とは限りなく近づくものの、決して交わったり接したりしない線のことです。
例題を使って、実際に反比例のグラフをかいてみましょう。
| <例題> y=12/xのグラフをかきなさい。 |
グラフをかく手順は、次のとおりです。
2.取った値をグラフ上にプロットする。
3.点をなめらかな曲線でつなぐ。
順に進めていきましょう。
まず「1. 反比例を表す式が成り立つようなx、yの組み合わせをつくる」ためには、式を表にすると簡単です。
y=12/xのグラフを表にすると、次のようになります。
| x | -12 | -6 | -4 | -3 | -2 | -1 | 1 | 2 | 3 | 4 | 6 | 12 |
| y | -1 | -2 | -3 | -4 | -6 | -12 | 12 | 6 | 4 | 3 | 2 | 1 |
表はx、yがともに整数になる組み合わせだけを考えればOKです。整数でない値も存在してはいますが、グラフにプロットできないためです。
x、yの組み合わせが見つかったら、座標平面状にプロットしていきましょう。
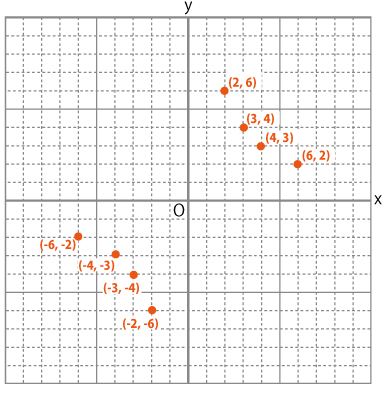
点が取れたら、なめらかな曲線でつなぎます。
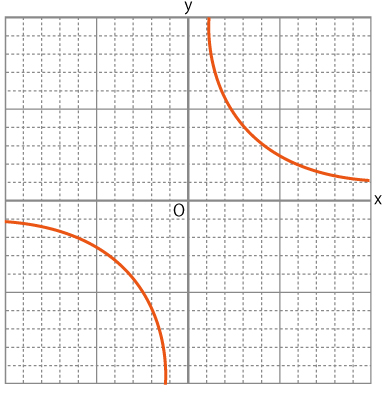
これで反比例のグラフがかけました。
(3) 変域
「変域」とは値が変化する範囲のことです。関数のグラフは基本的にどこまでも続いていきますが、変化する範囲を定めたいときに変域を利用します。
例題を使って変域の考え方を解説します。
| <例題> 反比例 y=24/x において、xの変域が2≦x≦6のときの、yの変域を求めよ。 |
まず、ざっくりとグラフの形をとります。y=24/xは、a>0なのでグラフは第1象限・第3象限に置かれます。
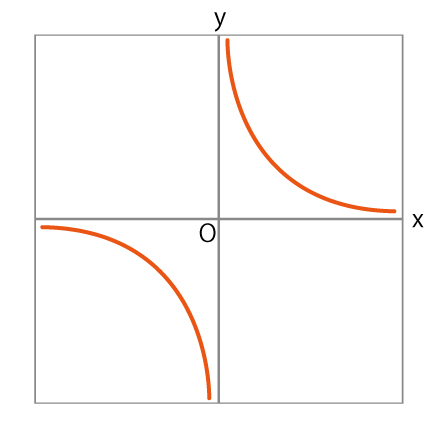
この形になることを押さえましょう。
xの変域は2≦x≦6なので、対応するyの値は第1象限にあるとわかります。第1象限にあるyの値は、xが最小のとき最大となり、xが最大のとき最小となります。
以上を踏まえて、xの変域2≦x≦6に対応するyの値を求めます。
y=24/xにおいてx=2のとき、
y=24/2
y=12
x=6のとき、
y=24/6
y=4
つまりyの変域は、4≦y≦12となります。グラフに表すと、次の範囲です。
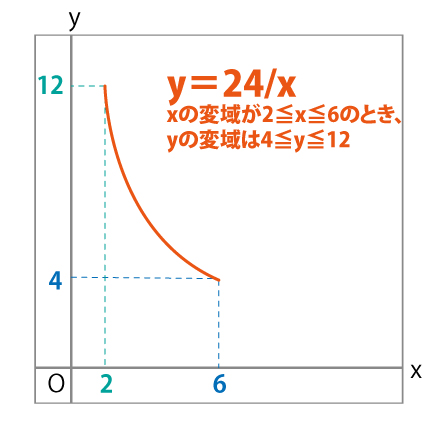
反比例を理解するポイント

反比例は「関数」という分野の1単元です。反比例をはじめとする関数は、苦手とする中学生も多いようです。なぜ、関数は苦手とされやすいのでしょうか。その原因と、克服のポイントをまとめました。
(1) 苦手の原因:「関数とは何か」を理解していない
関数とは、「ともなって変化する」数量関係といわれます。一方の量(x)を決めると、他方の量(y)が決まる関係です。この基本概念の理解を曖昧なままにすると、この先の学習が「何をしているのかわからない」状態になってしまいます。まずは、関数とは何かを丁寧に、納得いくまで考えていきましょう。
意外と身近な関数
世の中には、ある値が、他の値の影響を受けて決まるケースが、よくあります。踏切を電車が通過する時間は、通貨列車の車両数によって決まりますよね。エアコンの最適な設定温度は、外気温によって決まるのも1つの例です。
関数は、この「ともなって変化する」値の仕組み、関係性に注目した単元です。関係性に注目している、というのが大きなポイントです。
関数と他の単元の違い
他の単元は、どれも「値そのもの」を扱います。方程式も図形も、値を決めることをゴールにしていました。ところが、関数が扱うのは、事象の関係性です。他の単元と同じように、数字をいじっていけば答えの値が出る、という単元ではないのです。
関係性に注目するという意味では、規則性とも通じる部分があります。もしかして、関数が苦手なお子さんは、規則性も苦手ではないでしょうか。
そもそも、着目するポイントが他の単元とは違う、という点の納得が関数の克服には重要です。
(2) 克服法(その1):いま、何の操作をしているか考えながら解く
関数が苦手な中学生は、「先生が言うがまま」「解説に書かれているまま」、ノートに写そうとするケースが多いようです。
「問題文にこう書かれているから、式はこうなるね」「この式を解くと、こうなるね」と、先生や解説の誘導のままに、取り組みます。一見、素直に取り組んでいるように見えますが、ここが注意ポイント。何も考えずにノートに写しても、決して関数はできるようにはなりません。
先に、関数は「関係性を見出す単元」である、と解説しました。つまり、関数単元の最終的なゴールは、関係性を自力で見出せるようになること、です。問題文で与えられた状況を整理し、自分で考え、ともなって変わる関係性を見つけて、式に起こせるようになって、はじめて解けるのです。
一つひとつのプロセスを、「いま何をしているのか」「何に向かって進んでいるのか」と考えながら取り組む姿勢を意識していくことが重要です。
(3) 克服法(その2):なぜ、その解き方だったのかを考える
解けなかった問題や間違えた問題の復習も、(2)と同様です。解説を見て、丸写しするだけでは克服できません。解説の一行一行について、「なぜ、こう操作するのか」「なぜ、この解き方なのか」を考え、納得する過程を大切にします。
学年が進むと、一次関数・二次関数と、さまざまな関数が登場します。テストや入試の問題では、「そもそも、この問題は関数なのか」「関数だとしたら、どの関数なのか」を判断する力も求められるようになります。「解説に反比例と書いてあるから、反比例で解く」と取り組んでいても、実力アップは望めないでしょう。なぜ、どうしてという本質的な問いを、いつでも念頭に置いておくようにします。
反比例の基本問題をマスターしよう

ここからは、反比例の基本的な典型問題を2種類解説します。反比例は比例に比べて見慣れないため、数値の関係をよく見て「反比例かどうか」判断できることが大切です。
前の章で解説した「何の操作をしているのか考えながら解く」「なぜ、この解き方をするのか考える」といった姿勢も意識してみてください。
(1) 反比例を判断する問題
テストでもよく出題される、反比例を判断する問題を解いてみましょう。
| <例題> 次の2つについてyをxの式で表し、反比例といえるか答えなさい。 1. x円の商品を買い、1000円札を出したときのお釣りy円。 2. 100km離れた場所まで時速xkmで進むときにかかる時間y時間。 |
<考え方>
「yをxの式で表し」との指示に従い、まずyをxの式で表してみましょう。式がy=a/xのかたちになっていれば反比例です。
1. お釣りは、1000円札から買った商品代金を引いた残りです。
従ってお釣りy円は、次のように表わせます。
y=1000-x
これはy=a/xではないため、反比例ではありません。
1次関数はy=ax+bという形です。y=1000-xを変形すると、y=-x+1000となり、まさに1次関数と同じですね。
1次関数は高校入試でもかならずといっていいほど出題される、中学数学最重要単元の1つです。いま学んでいる反比例で、1次関数の土台となる「関数の考え方」をしっかり身につけましょう。
2. 道のりと速さを表す問題です。
速さ×時間=道のり
この公式を思い出しましょう。
問題文から、以下の情報が分かっています。
速さ 時速xkm
時間 y時間
道のり 100km
この3つを式に表すと、
x×y=100
y=の形に変形して、
y=100/x
これはy=a/xのかたちになっていますね。
よって、反比例といえます。
(2) 反比例の式を求める問題
反比例の式を求める問題も練習しましょう。同じように例題を使って、考え方を解説します。
| <例題> yはxに反比例し、x=5のときy=8である。このとき、yをxの式で表しなさい。 |
<考え方>
「yはxに反比例し」とあるため、求める式の形は
y=a/x
です。
これを念頭に置き、与えられている値を代入しましょう。
x=5、y=8を代入すると、
8=a/5
a=40
比例定数a=40と分かりましたね。
反比例の式に代入して答えを出します。
答え y=40/x
上の計算では、x=5、y=8を掛け合わせるだけでaを出せます。いちいち分数を使わなくて済むため、計算ミスも防げます。
「かけ算の方が考えやすい」という人は、こちらの方法も使ってみてください。
反比例の応用問題

いよいよ、反比例の学習も最終段階です。応用問題、つまり文章問題にチャレンジしましょう。反比例は該当する事象の数が多くはないため、比例ほど文章問題のバリエーションがありません。
反比例の文章問題のうち、典型的な3つのパターンを解説します。
(1) 水槽に水を入れる
水槽に水を入れる問題は、関数分野ではよく登場します。反比例になる問題を見てみましょう。
| <例題> 毎分5リットルずつ水を入れると、30分でいっぱいになる水槽がある。毎分xリットルずつ水を入れるとき、いっぱいになるまでy分かかるとして、次の問いに応えなさい。 1. yをxの式で表しなさい。 2. 毎分10リットルずつ水を入れると、水槽がいっぱいになるまで何分かかるか求めなさい。 3. 6分でこの水槽をいっぱいにするには、毎分何リットルずつ水を入れればよいか求めなさい。 |
<考え方>
文章題では、はじめに与えられた状況(情報)を整理するのが鉄則です。
今回、数値が明確にわかっている情報は「水槽に毎分5リットルずつ水を入れると、15分でいっぱいになる」です。
ではこの水槽には、結局何リットルの水が入るのでしょうか?
満タンの量=毎分5リットル×30分
つまり、水槽は150リットルだということもわかりますね。
以上の情報を使って、問題を解いていきましょう。
1. yをxの式で表すためには、以下の情報を使います。
水槽全体の水量 150リットル
1分間に入れる水量 xリットル
満タンまでの時間 y分
つまり、
xy=150
y=150/x
これでyをxの式で表せました。確かに反比例の形をしています。
2. 以降は、1.で作ったy=150/xを使って解いていきます。
2.の問題は「毎分10リットルずつ水を入れると、水槽がいっぱいになるまで何分かかるか」ですね。
y=150/xの式において、yが表すのは「水槽が満タンになるまでの時間」です。xは「1分間に入れる水量」を示します。今回は毎分10リットルずつ水を入れるため、x=10ですね。
代入してみましょう。
y=150/x
y=150/10
y=15
したがって15分で満タンになるとわかりました。
3.の問題は「10分でこの水槽をいっぱいにするには、毎分何リットルずつ水を入れればよいか」ですね。2と同様に考えれば解けますよ。
y=150/xの式において、yが表すのは「水槽が満タンになるまでの時間」です。今回はこれが6分とわかっています。xは「1分間に入れる水量」で、こちらが今回は求める数値になります。
代入してみましょう。
y=150/x
6=150/x
x=25
したがって毎分25リットルずつ入れればよいとわかりました。
(2) 速さと時間
比例につづき、反比例でも道のりや速さを題材にした問題が登場します。例題を見てみましょう。
| <例題> 太郎くんの家から学校までの道のりは1200mあります。分速xmで学校に行くときにかかる時間をy分とします。次の問に答えなさい。 1. yをxの式に表しなさい。 2. 学校に10分で着くためには、どのくらいの速さで学校に行けばよいか答えなさい。 |
<考え方>
1. 道のりや速さの問題では、まず次の公式を余白にメモしましょう。
道のり=速さ×時間
今回、問題からわかっている情報は次のとおりです。
道のり 1200m
速さ 分速xm
時間 y分
この3つを、公式に当てはめます。
道のり=速さ×時間
ですから、
1200=x×y
問題文では「yをxの式で表す」と指示があります。式を変形して、
y=1200/x
これで答えがでました。
2. 「学校に10分で着くためには、どのくらいの速さで学校に行けばよいか」は、1.で出た式を使います。
今回、求めたいのは「速さ 分速xm」の部分です。かかる時間 y分は10分と分かっています。y=1200/xに、y=10を代入すると、
10=1200/x
x=120
つまり分速120mで学校に行けばよいということがわかりました。
(3) 仕事の量
仕事の量に関する問題も見てみましょう。
| <例題> 2人で進めると98日かかる仕事がある。急ピッチで進めたい状況になり、7日で完了させる必要が出てきた。何人で取り掛かれば終わるか、求めなさい。 |
まず「2人で進めると98日かかる」という情報から、必要な人手の延べ人数を求めます。
2人×98日=196
つまり、この仕事は延べ196人が必要だとわかりました。式にしてみましょう。
最終的に求めたいのは「人数」のため、人数をyとします。必要な日数をxと置きましょう。
先ほど出した仕事の総量より、
x(日)×y(人)=196
y=196/x
問題文より「仕事を7日で終わらせたい」のですから、x=7を代入して、
y=196/7
y=28
答え 28人
・人数が2倍になれば、かかる日数は半分になる
・かける日数が2倍にばれば、必要な人手は半分になる
つまり仕事の総量は一定であるため、人数と日数のどちらかが増えれば、他方は減るということです。これはまさに反比例の良い例です。
ちなみにこの時に考えている「人数」は延べ人数であることに注意しましょう。1人が2日働いた場合は「2人」と考えます。
反比例を得意にする勉強法

反比例は登場する頻度こそ多くないものの、関数分野の土台をつくる大切な単元です。伴って変わる2つの数の関係性を見出す思考力は、中2の「1次関数」や中3の「2次関数」にもつながっていきます。
反比例を得意にしたい中学生におすすめの学習法を、4つ解説します。
(1) グラフを正しくかけるようにする
反比例のグラフは、双曲線と漸近線を形どらなければなりません。慣れるまでは点を滑らかにつなぐのが難しく、カクカクしたグラフになりがちです。
しかし反比例のグラフは「滑らかな曲線であること」が重視されます。ただし、滑らかなグラフでもプロットした点を通っていなければ減点されます。
テストまでに曲線グラフを上手にかけるよう練習しておきましょう。
はじめのうちは、方眼ノートを使うと書きやすいでしょう。さまざまなサイズの方眼ノートが市販されています。店頭で使いやすそうなものを探してみてください。
また、1ページごと切り取れるタイプのノートは、書いたグラフを切り取って別のノートに貼りつけたり、問題集に挟んだりもでき、活用の幅が広がります。
(2) 計算は丁寧に進める
反比例の式は「y=a/x」でした。分数の形をしているため、必然的に計算過程でも分数が登場します。
分数はそうでない式に比べて計算ミスが起きがちです。分数を整数の形にする方法や、左辺と右辺の合わせ方など、間違えないよう丁寧に進めましょう。
分数の計算方法に不安がある人は、小学校で学んだ分数の単元を復習してみてください。
またy=a/x は xy=aと変形すると、分数の計算を回避できます。計算ミスを減らす、おすすめテクニックです。
「ちびむすドリル 小学生」から、小6の分数の単元をチェックしてみてください。問題のプリントと回答が、すべて無料で利用できます。
(3) 文字に置いた要素同士の関係をつかむ
反比例の問題を解く際は、次の点に注意しましょう。
・問題文中のどの要素を文字に置いたか
・文字に置いた要素同士の関係性はどのようか
関数は「伴って変わる数の関係性」を式にしたものです。つまり「伴って変わる数」と「関係性」が分かって、はじめて問題が解けます。
水槽の問題なら「水を入れてからの経過時間と、溜まった水量の関係」、速さと道のりの問題なら「出発からの経過時間と、進んだ距離」など、かならず伴って変わる数と関係性が存在します。
ここをあいまいにすると、解いている最中に「今、何をしているのか」迷子になりやすくなります。文字に置いた要素や関係性を余白にメモする、下線を引いておくなどわかりやすくする工夫をしながら、解き進めてみてください。
反復学習のためにも、教科書や問題集への書き込みは避けたほうが良いでしょう。ただ、ノートやプリントは、どんどん書き込んで構いません。「こうかな?」「それとも、こうかな?」と書き込み、試行錯誤しながら、答えにたどり着く練習を重ねてください。
(4) 自力での対策が難しい場合は塾や家庭教師を利用する
反比例は概念の理解が難しい単元です。
「式にあてはめて計算するだけならできるが、文章問題になると解けない」と苦戦する中学生は、もしかするともっとも大切な概念理解ができていないかもしれません。「片方が増えるともう片方も増える」比例は直感的に理解しやすいのですが、「片方が増えるともう片方が減る」反比例は実感を伴った理解を得にくいのが原因です。
ただし反比例の概念は関数分野全体の理解にも影響を及ぼすため、しっかりと理解し定着させておくのが望ましいです。
もし自力での反比例学習が難しいと感じたら、塾や家庭教師などプロの力を借りましょう。反比例は講師によって着眼点や解き方が異なる分野で、相性が合うとまさに「目から鱗が落ちる」ほどの理解が得られます。
相性の合う塾探しには「塾探しの窓口」をご利用ください。お住まいの地域と学年を入力するだけで、実際に利用した方から高く評価されている教育サービスを検索できます。
中1生の数学対策におすすめの個別指導塾5選

反比例の全体像は、およそ理解できたでしょうか。しかし、定期テストの結果につなげるためには、「わかったつもり」を「本当に理解した」状態に、さらに「自分の力だけでできる」レベルに高めなければなりません。
考え方やアプローチが難しい反比例、そして関数の習得は、プロの指導を受けることが近道です。「つまり、どういうことか」と本質を丁寧に解説してくれる塾を選び、得点源に育てていきましょう。
ここからは、中学1年生の数学対策、さらに高校受験までの指導力に定評ある個別指導塾を厳選して5つ紹介します。
個別教室のトライ
抽象概念の理解が必要な関数は、「考え方」を習得する段階がもっとも難しいといわれます。関数の考え方を、丁寧にじっくり解説してもらいたい中学生には、マンツーマン指導が最適。すべての授業をマンツーマンで提供する、個別教室のトライに相談してみてはいかがでしょうか。
個別教室のトライは、塾業界屈指の140万人もの指導実績を誇ります。膨大なデータから導かれた、効果的かつ効率的な勉強法「トライ式学習法」は、困っていた勉強の悩みを解決してくれると評判です。
自宅でトライの指導を受けられるサービスもあります。トライのオンライン個別指導塾は、完全リモートの授業を展開しており、自宅受講が可能です。高品質な指導をリーズナブルに受けられるとあって、いま人気が高まっています。
個別教室のトライの料金情報は、以下のとおりです。
| 入会金 | 11,000円 |
| 授業料(目安) | 26,000円~30,000円/月 |
| その他の費用 | 季節講習あり(中学生は35,000円~70,000円程度) ※ 教材費は不要 |
無料資料請求する
東京個別指導学院・関西個別指導学院
東京個別指導学院・関西個別指導学院は、生徒一人ひとりに徹底的に寄り添った、親身な指導に定評ある塾です。学習計画や授業のペースは、生徒と相談しながら決定するため、無理や無駄がありません。講師1人が生徒2人を指導する1対2スタイルで、授業時間内で解説の時間と演習の時間をバランス良く確保できます。
「生徒ファースト」を掲げるだけあり、細部にいたるまで勉強のしやすさにこだわるあり方も、東京個別指導学院・関西個別指導学院の強みでしょう。集中できる工夫が凝らされた自習室や、欠席連絡の期限は授業直前までOKという点も、中学生にとって嬉しいポイントです。
東京個別指導学院・関西個別指導学院の料金情報は、以下のとおりです。
| 入会金 | なし |
| 授業料 | 受講教科や回数、ペース、使用教材などによって変動 要問合せ |
| その他の費用 | 季節講習あり |
無料資料請求する 最短1分で完了! 関西個別指導学院のお近くの教室に
無料資料請求する
個別指導WAM
「せっかく塾に通うなら、すぐに定期テストで結果を出したい」、そう考えるのは自然なことです。次のテストから結果を出すなら、個別指導WAMが最適!個別指導WAMは、教室近隣の中学校事情に精通しており、定期テストの出題傾向に合わせた指導を得意とします。
定期テストの2週間前からは、通常授業とは別の日程でテスト対策を実施します。受講している数学以外の対策も受けられるため、5教科の総合的な成績アップも狙えます。
オンライン家庭教師WAMは、個別指導WAMと同様の指導を、自宅で受けられるオンライン指導です。専用システムを使った授業は、対面授業と遜色ないと好評を博し、受講する生徒が増えています。
個別指導WAMの料金情報は、以下のとおりです。
| 入会金 | 入会金と登録料が必要、金額は要問合せ |
| 授業料 | 中1・2:7,600円~ 中3:8,400円~ ※週1回・40分コースの月額 |
| その他の費用 | 年会費 維持管理費(毎月) e-ラーニング教材費 |
※ 返金制度あり
最短1分で完了! 個別指導WAMのお近くの教室に無料資料請求する
代々木個別指導学院
「何から始めればいいのかわからない」「勉強の仕方がわからない」といった、漠然とした悩みを抱える中学生も多いでしょう。そんなときは、代々木個別指導学院に相談してみてください。代々木個別指導学院は、一人ひとりの生徒と真摯に向き合い、その生徒のためだけにカリキュラムや指導を実践する塾。習熟度や考え方の癖まで踏まえた、本当にすっきりと理解できる授業を受けられます。
数学で起こりやすい「わかったつもり」を防ぐ勉強法や、暗記の効率を上げる取り組み方など、代々木個別指導学院ならではのメソッドも豊富。数学以外の教科にも生きる、本当に正しい勉強法を習得できます。
代々木個別指導学院の料金情報は、以下のとおりです。
| 入会金 | 20,000円 |
| 授業料 | 10,800円~/1科目 |
| その他の費用 | 季節講習あり(30,000円~40,000円程度) |
無料資料請求する
ナビ個別指導学院
「数学に自信がない」という中学生は、お近くのナビ個別指導学院の体験授業を受けてみてください。ナビ個別指導学院は「褒める指導」の実践で知られる個別指導塾で、日々生徒と接する講師は、褒めるスキルを伸ばす研修も受けています。些細な努力や成果も褒めてもらえるため、徐々に数学への自信を取り戻せるはずです。
学習計画は、中学生本人と保護者の方の話をじっくりと聞いた上で、個別に作成します。復習に力を入れたい、受験レベルにまで実力を高めたいなど、どのような相談にも誠実に対応してもらえます。
ナビ個別指導学院の料金情報は、以下のとおりです。
| 入会金 | 22,000円 |
| 授業料 | 中1・2→12,600円 中3→16,800円 ※ 週1回授業を受けた場合の月額 |
| その他の費用 | 諸経費 3,480円/月 季節講習あり(コマ単価3,700円~3,800円) |
無料資料請求する
まとめ
反比例は「一方が2倍、3倍…になると、もう一方が1/2、1/3…になる」関係を持つ関数です。比例の反対としてセットで学びますが、比例より反比例のほうが苦手意識をもちやすいため注意しましょう。
反比例をマスターするコツは、変化する2つの要素の関係を正しくつかむことです。幸いにも反比例の文章問題はバリエーションが多くありません。学校のワークに載っている問題を習得すれば、定期テストや高校入試にも十分対応できます。「反比例をやらなきゃ」と思ったこの機を逃さず、一気にマスターしてしまいましょう。
もし自分の力だけでは頓挫してしまいそうな場合は、遠慮なく塾や家庭教師の力を借りるのがおすすめです。



中学生向けのおすすめ塾
中学生向けの塾の料金・口コミ
- 個別教室のトライの料金・口コミ
- 東京個別指導学院・関西個別指導学院の料金・口コミ
- 代々木個別指導学院の料金・口コミ
- 個別指導WAMの料金・口コミ
- ナビ個別指導学院の料金・口コミ
- 中高一貫校専門 個別指導塾WAYSの料金・口コミ
- スタディコーチの料金・口コミ
- 坪田塾の料金・口コミ
- 個別指導塾トライプラスの料金・口コミ
- 個別指導学院サクシードの料金・口コミ
- 個別指導スクールIEの料金・口コミ
- 個別指導塾スタンダードの料金・口コミ
- 個別指導塾サクラサクセスの料金・口コミ
- ドリームホームスクールの料金・口コミ
- みやび個別指導学院の料金・口コミ
- ITTO個別指導学院の料金・口コミ
- コノ塾の料金・口コミ
- 学習空間の料金・口コミ
- キズキ共育塾の料金・口コミ
- 森塾の料金・口コミ
- 自立学習REDの料金・口コミ