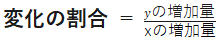【中2数学】中2で習う単元まとめ | 勉強のコツをご紹介

中2は、中1で学んだ数学の基礎をさらに発展させていく学年です。連立方程式、１次関数は必ずおさえておきましょう。また図形の「証明」を新しく学びます。

ここでは中2数学で学ぶ内容とポイントについて紹介します。

あわせて、中学生の数学対策におすすめの塾5選もまとめました。お子さんに合う塾に出会い、数学を得意教科にするヒントとしてご活用ください。

中2で習う数学の概要

中1までの数学は、「思い浮かんだ公式に、なんとなく数字を当てはめて解く」手法でもそれなりに得点できたかもしれません。しかし中2になるといよいよ内容を本質的に理解していないと、手足が出ない問題が増えてきます。

また中2数学で習うほぼすべての単元は、高校入試でかならずといって良いほど出題されます。高校入試数学の三大重要単元ともいわれる「1次関数」「連立方程式」「図形の証明」も、すべて中2の学習範囲です。

中2の数学は、習う一つひとつの内容が高校入試に直結していると意識して臨みましょう。

「本質的な理解が重要」「高校入試頻出の単元が登場」という中2数学のポイントは、テストにおいて記述形式で解答させる問題の増加という形であらわれます。答えだけでなく解答に至るプロセスも採点対象になり、さらに解答も数学的表現・論理的に正しい記述で書くように求められます。

中2の数学は、中1に増して「しっかり理解する学習」を心がけてください。

勉強の注意点

中2の数学では、単元の基本を学習した後に登場する発展問題に注意が必要です。「○○の利用」と名前がつく項目が該当し、たとえば「連立方程式の利用」「1次関数の利用」などがあります。

「○○の利用」は名前のとおり、直前に学習した単元の基本を使い応用的な問題を扱います。いわゆる文章題です。

中2数学の文章題が厄介なのは、問題文の読解と数学的思考を同時に駆使しないと解けない点にあります。

具体的な問題を見てみましょう。次は「連立方程式の利用」の典型である速さに関する問題です。

もう1つ、問題を見てみましょう。次は「1次関数の利用」の典型で、苦手とする中学生が多い「水量」に関する問題です。

これらの問題を解くためには、「何が起きているのか」という事柄の関係を読み解きつつ、記号に置くべき情報を決め、数式に表現する数学的論理力が必要です。

文章題を例に解説しましたが、中2の数学はすべての単元において数学的論理力の養成を重視しています。

中2の数学を勉強する際は「いま、自分は何を求めるために・どのような操作をしようとしているのか」を常に意識するようにしましょう。公式を使うときも「なぜこの問題にこの公式を使うのか」「この公式は何を求める式なのか」と、考えて学習するよう心がけましょう。

１．式の計算

中1で学んだ文字式の計算から発展したものを学びます。

（１）式の計算の用語

中1で学んだものも含みます。

・単項式

文字や数の乗法だけでできている式のこと。（なお除法も「逆数をかける」ことで乗法とみなされるためこの表現となります）

（例）－5abc　x³yz

・多項式

単項式の和（加法）で表された式のこと。（なお差（減法）も「負の数を足す」と考えられるためこの表現となります）

（例）a²－2ab＋b²

・項

多項式の、＋や－でつながれているひとつひとつの単項式を「項」と呼びます。

・同類項

まったく同じ文字をもつ単項式を同類項といいます。同類項どうしは足したり引いたりでき、「同類項をまとめる」といいます。

（例）－5abc＋15abc       ＝（－5＋15）abc
　　　　　　　　　　　　＝10abc

・係数

単項式において、かけられている数字を計数といいます。例えば5xの係数は5です。

・次数

単項式において、かけられている文字の数を次数といいます。例えば5ab³cdはaが1個、bが3個、cが1個、dが1個あるので、合計で文字は6個＝6次式となります。

・多項式の次数

項が複数ある多項式では、各項のうち最も次数の大きい項が、その多項式の次数となります。

（例）x⁴－2ab＋b²　←次数は4

・１次式

次数が1の式をいいます。次数が2は2次式、3は3次式とよぶこともあります。「1次方程式」の1次はこれをさしています。

（２）式の加法、減法、乗法、除法、いろいろな多項式の計算

・式の加法、減法

中1で習った文字式の足し算、引き算をさらに発展させたものです。式と式を足し引きする場合は、それぞれの式に（）をつけてから行います。最後は「同類項」をまとめて式を整理します。

【加法の例】

10x-8yと 15x+2yをたしなさい。

(10x－8y)＋(15x＋2y)　＝10x－8y＋15x＋2y　       ←足し算はそのままかっこをひらく
　　　　　　　　　　　＝10x＋15x－8y＋2y　       ←同じ項でそろえる
　　　　　　　　　　　＝(10＋15)x＋(－8＋2)y　  ←数字をまとめる。負の数の計算注意
　　　　　　　　　　　＝25x－6y

【減法の例】

－が（）の前にあるとき、（）の中の符号は逆になることに注意！

筆算のように縦書きにして（同類項を縦にそろえて）、計算することもできます。

・単項式の乗法、除法

単項式どうしのかけ算、わり算です。分配法則を使います。

【例】

－5(4a＋5)　＝－5×4a＋(－5×5)
　　　　　 　＝－20a－25

（３）文字式の利用（式を利用した説明）

身の回りの数に関わる性質について、それが一般的に成り立つかどうかを、文字式を利用して説明することができます。与えられた文章にある情報を文字式に表せるかどうかがポイントです。

式の計算、文字式は、計算練習を何度も繰り返し、見ただけでミスなく正解できるようにしましょう。また計算の途中式は必ず書き残す癖をつけてください。

２．連立方程式 

中2の最重要単元のひとつです。高校入試でもほぼ必ず出題されます。手順や問題パターンを身につけて得意分野にしましょう。

（１）連立方程式とは

・2元1次方程式とは

通常、「方程式」という場合、含まれる文字は一種類（1つ）だけです。これに対し、2元1次方程式とは、文字が2つ使われている1次方程式をさします。

通常の方程式（1次方程式）は、解があります（中1の単元）。しかし、2元1次方程式を成立させる解は無限にあり、解は一つに定まりません。

・連立方程式とは

2つ以上の方程式を組み合わせたものを連立方程式とよびます。このとき、どの方程式も成り立たせられる解がある場合、それを連立方程式の解といいます。

なお、中学で習う連立方程式は「2元1次方程式が2つあるもの」で、この場合は解は1組に定まります。

・連立方程式の解の確かめの方法

求めた解をあてはめていずれの式の計算結果も成り立てば、その解は正しいことになります。

（２）連立方程式の解き方①「加減法」

x、またはyの係数をそろえ、2つの式を足すか引くかして、片方の文字を消す方法です。その後、一つの文字が決まれば、元の式のどちらかにその数字を代入して、残った文字の数も求め、解を求めます。

係数が同じものがある場合はそちらを足し引きして０にします。係数が同じではない場合は、片方または両方の文字の係数を最小公倍数でそろえます。

（３）連立方程式の解き方②「代入法」

片方の式が「x（またはy）＝…」の形になっていた場合、x（またはy）の値を先に求め、それを残ったもう片方の式にあてはめて一つの文字の式にして解を求める方法です。

（４）連立方程式の利用

文章問題を連立方程式を使って解いてみましょう。中1のときに学んだ1次方程式の文章題と同じく、「何を文字にするか」がポイントになります。連立方程式ではxとyなど、2つの文字が必要です。

３．１次関数

1次関数は、中1の時に学んだ「比例」を発展させたものです。比例は必ず原点Oを通る直線のグラフになりますが、1次関数ではグラフのy軸のどこに交わるかを、方程式との関連で考えていきます。

（１）1次関数とは

2つの変数xとyがあるとき、yをxの1次式で表せる関数を1次関数といいます。

「関数」については中1の単元を復習してください。

（２）１次関数の値の変化と「変化の割合」と「傾き」

xが1増えたとき（＝xの増加量）に、yがいくつ増加するか（＝yの増加量）を「変化の割合」といいます。1次関数では、変化の割合は以下の式で求められます。

（３）１次関数からグラフを書く

・「切片」とは？比例のグラフと1次関数のグラフを比較

1次関数の式「y＝ax＋b」で、b＝0のときを考えると、y＝ax、つまり中1で学んだ比例の式になります。b＝0のとき比例のグラフは原点Oを通りました。

1次関数の式におけるbは、この式がy軸のどの点と交わるかを表しています。このy軸と交わる点（0, y）を「切片」といいます。

・「傾き」とは？傾きと変化の割合の関係

「変化の割合」を1次関数の「傾き」といいます。その名前のとおり、グラフ上では直線の傾きとして見えます。変化の割合が大きければ大きいほど、直線の傾きは急になります。

・1次関数の式から傾きと切片を読み取り、グラフをかく

1次関数の式をグラフに書くときは切片をとり、傾き（変化の割合）をもとに2点目をとって直線で結びます。

・「xの変域」が決まっているとき、「yの変域」を求める

変域とはその変数の取り得る幅です。xの変域はグラフでは横の幅で表れ、yの変域はグラフ上では縦の幅で表れます。

（４）グラフから１次関数の式を求める

式からグラフを書くのではなく、グラフから1次関数の式を求めるには、以下の3つの方法があります。

（５）方程式ax＋by＝cのグラフを考える

y＝ax＋bの形になっていない1次方程式の場合、移項などを使ってy＝ax＋bの形に変形します。

（６）連立方程式とグラフの関係

「連立方程式の解と、グラフの交点の座標との関係」 「2直線の交点の座標を連立方程式で求める」などを学びます。

（７）１次関数の利用

１次関数を利用して文章題を解きましょう。また1次関数のグラフを利用した問題もあります。

４．図形の性質

中2では図形の性質や面積・体積の求め方を基礎として、証明問題までを学びます。中1で学んだ用語、事項や作図方法なども復習しておきましょう。

（１）角と平行線の性質

・対頂角

2直線が交わってできる向かい合う角を対頂角といいます。対頂角は等しい大きさになります。

・平行線と同位角

2直線mとn両方に交わる直線があるとき、それぞれの直線がつくる8つの角のうち、同じ方向にできる角を同位角といいます。同位角は等しい大きさになります。

・平行線と錯角

2直線mとn両方に交わる直線があるとき、それぞれの直線の内側にできる四つの角のうち、斜め向かいにある角どうしを錯角といいます。錯角は等しい大きさです。

（２）三角形の角の性質

三角形の角には以下の性質があります。

・用語

何を指すか正しく覚えましょう。

（３）多角形の角の性質

多角形の角には以下の性質があります。

（４）三角形の合同条件

・合同とは？

2つの図形があるとき、この2つがぴったり重ね合う場合に2つの図形は合同であるといいます。

・三角形の合同条件

５．図形の性質と証明

中学からの数学で、小学校までと最も違う新しい単元が「証明」です。考え方もですが、証明問題の書き方自体のルールも覚えて再現できるようにしなければなりません。

（１）証明問題とは

証明問題を学ぶために、以下の用語を理解しておきましょう。

（２）二等辺三角形と正三角形、直角三角形

・二等辺三角形の性質

【定義】

2辺が等しい三角形を二等辺三角形といいます。等しい長さの2辺の間の角を頂角、それ以外の2つの角を底角といいます。

【定理】

二等辺三角形の底角は等しくなります。

二等辺三角形の頂角の二等分線は、底辺を垂直に等分する垂直二等分線になります。

【二等辺三角形になるための条件】

三角形において、「2辺の長さが等しい」または「2つの角の大きさが等しい」ときに二等辺三角形になります。

・正三角形の性質

【定義】

3つの辺の長さが等しい三角形を正三角形といいます。

【定理】

正三角形の3つの角の大きさは等しくなります。

・直角三角形の性質

【定義】

1つの角が直角である三角形を、直角三角形といいます。直角の向かい側にある辺（最も長い辺）を「斜辺」といいます。

（３）平行四辺形

・平行四辺形の定義

2組の向かい合う辺がそれぞれ平行な四角形を、平行四辺形といいます。

・平行四辺形の性質

平行四辺形には以下の性質があります。

・平行四辺形になるための条件

平行四辺形の性質から、平行四辺形の条件が導き出せます。次の条件のうち、いずれかが成り立てば平行四辺形になります。

（４）いろいろな四角形と平行線

平行線と面積の関係を扱った問題に「等積変形」などがあります。

・底辺が共通な三角形は高さが同じのため面積が同じになる

・同じ平行線の上にある四角形の面積は底辺の長さに比例する

を利用します。

６．場合の数と確率

「場合の数」「確率」は小学校でも少し学んでいます。数学問題としての確率をマスターしましょう。

（１）確率とは

・「同様に確からしい」とは

ある事柄において、起こりうる結果のそれぞれが同じ程度に期待できるとき、どの結果も「同様に確からしい」といいます。

例えばサイコロをふるとき、何か細工がされていない正方形のサイコロでは、どれか1つの目だけに偏って出やすくなることはないと考えられます。最初の10回程度サイコロを振ったときには、もしかしたら6が10回中3回出ることもあるかもしれませんが、何千回、何万回と試行すると、どの目も同じくらいの「程度」になっていきます。このようなとき、サイコロでどの目が出ることも「同様に確からしい」といえます。

・確率とは

ある事柄が起きると期待される「程度」を数で表したものを、その事柄の起きる「確率」といいます。上の例では、サイコロの6の目が出る割合が「確率」です。英語では probability と表します（頭文字のpを「ある確率をpとする」などのように使います）。

・確率における「相対度数」とは

「確率」はある事象における起こり得る予想の割合であり、「相対度数」は統計上のデータで実際に示される事象の割合の傾向を示すものです。

確率pがあるとき、実際に同じ試行を何回も繰り返すと、ある事象の起こる相対度数が確率pの値に近づきます（上のサイコロの例を参照）。

・「確率pの値の範囲」および「p＝1、p＝0」の意味

ある事象の起こる確率をpとするとき、確率pの値の範囲は「0≦p≦1」となります。

必ず起こるときは確率p＝1、 一度も起こらないときは確率p＝0と表されます。

（２）確率の求め方

ある事象が起こりうる「場合（考えられる全てのパターン）」が全部でn通りあり、どの場合が起きることも「同様に確からしい」とき、場合がa通りあるならば、確率は「p＝a/n」で表されます。

つまり、確率を求めるには、「n＝何通りあるか」と「a＝起こる回数」を確実に数え上げる必要があります。

確率を求めるための数え上げには以下の方法があります。

７．データの活用

以下の用語を理解しましょう。

(1)「考えながら」問題を解く

数学の問題を解く際は、「いま自分は何をやろうとしているのか」と考えるようにしましょう。

中2になると、問題を解き始めてから解答に至るまでの過程が中1より長くなります。1問を解くのにノート数行、十数行を使うケースも珍しくありません。

何行も数式を書き続けていると、何が起きるか。「自分はいま、何を求めようとしていたのか」が分からなくなるのです。問題を解いていて迷子になる感覚、ともいえるでしょう。

一度迷子になると、また最初にもどって解法の方針と求めるべき要素を確認しないといけません。手間がかかり面倒な気持ちになりやすく、やがて数学への苦手意識につながります。

悪循環を防ぐためにも、問題を解きながら「何のために・どのような操作をしているのか」を考え続けるようにしてください。

(2)良質な問題集を繰り返す

苦手意識を持たず数学の成績を向上させるためには、問題演習量の確保が大切です。しかし、何冊もの問題集に取り組む必要はありません。

数学の成績を上げるためには、良質な問題集1冊を繰り返す学習が効果的です。

良質な問題集とは、以下の要素を満たした問題集を指します。

・お子さんのレベルや性格に合っている
・解説が詳しく書かれている
・例題は典型問題を網羅している
・練習問題が豊富に収録されている
・解説は取り外せる別冊形式が望ましい

お子さんが使いやすいビジュアルであることも大切な要素です。カラフルでイラストを多用した問題集を好むか、白黒でシンプルに解説された問題集を好むか、お子さんと一緒に書店で選定してあげてください。

もしどの問題集を使うべきか迷ったら、学校から配布された問題集を使えば間違いありません。また塾でお子さんに合う問題集を紹介してもらうのも良い方法です。

繰り返し学習で復習効率アップ！受験まで使える勉強法を解説

テスト範囲のお知らせをもらうと、必ずといっていいほど「繰り返し勉強しておくこと」という一言が書かれていることに気づき…

詳しく読む

印をつけるだけ！勉強の効率がみるみる上がる勉強法を解説

学力、あるいは成績は「できなかったことを、できるようにする」ことでしか伸びません。これが簡単なようでいて難しく、中学…

詳しく読む

(3)部活と両立できる勉強習慣を確立する

部活に力を注ぎたい生徒が増える中2は、部活と勉強の両立が課題になります。できるだけ毎日取り組みたい数学は、勉強時間をルーティンとして生活に組みこんでしまいましょう。

「学校の宿題の後」「夕食の後」「早朝」など、お子さんが取り組みやすい時間に数学学習の時間を確保します。1回の学習は10～15分で十分です。

短時間でできるプリント教材やドリルを用意しておくと、やることに迷わずスムーズに始められます。いま学校で習っている範囲や復習が必要な単元など、いくつかの種類を用意しておくと良いでしょう。

プリント教材は無料でダウンロードできるサイトから印刷すると便利です。

中2生が数学を学ぶならここ！おすすめの塾5選

本質的な理解と数学的な論理思考が欠かせない、中学2年生の数学。お子さんが、自分の力だけで勉強するのも、そろそろ難しくなってくるかもしれません。

数学に危機感を持ったら早めに塾に相談しましょう。ここからは、中学生の数学対策におすすめの塾を5つ紹介します。

(1) 個別教室のトライ

「計算過程を一つひとつ丁寧にチェックしてもらえる」「文章題の読み方、ヒントの見つけ方を一文一文教えてもらえる」、そんな細やかで丁寧な指導を受けるには、やはりマンツーマンの塾がベストです。全国650以上の教室で完全マンツーマン授業を提供する、個別教室のトライに相談してみませんか。

個別教室のトライでは、140万人以上の指導実績から編み出された、独自の「トライ式学習法」も指導します。高校受験、さらにその先にまで生きる勉強の土台を作りたい中学生にもおすすめです。

お近くに個別教室のトライがない方には、オンラインでの指導がおすすめです。トライのオンライン個別指導塾は、トライの対面指導と遜色のない品質の授業をオンラインで受講できます。

(2) 東京個別指導学院・関西個別指導学院

テストの結果も、もちろん大切。ただ、目標に向かって頑張る意義や、コツコツと努力を重ねる姿勢も身につけてほしい。我が子にそう願う保護者の方も、多いでしょう。そんな願いをかなえる塾が、東京個別指導学院・関西個別指導学院です。東京個別指導学院・関西個別指導学院は、きめ細やかな個別のサポートで、お子さんの学習意欲を伸ばし、チャレンジし続ける姿勢を育みます。

年ごろの中学生が自発的に勉強するには、「誰から教わるか」が大切です。東京個別指導学院・関西個別指導学院は講師との相性を重視し、本格的に授業が始まる前に複数講師との体験授業をセッティング。お子さんが信頼できると確信できた1人が、担任になります。

自由度が高いカリキュラムと時間割で、存分に数学の力を伸ばしていきましょう。

(3) 個別指導WAM

中学生にとって、定期テストの結果や内申点は、高校受験にも影響する大切な要素。毎回のテストで着実に結果を残してこそ、進路選択の幅が広がります。数学の定期テストでしっかりと結果を出したい中学生は、お近くの個別指導WAMに相談してみましょう。

個別指導WAMは、地域の学校に合わせた授業を得意とする塾です。学校の授業進度やテスト範囲にピッタリ合った授業で、数学への理解が深まります。授業の中では正しい勉強法も指導します。数学の問題演習も効果的に取り組めるようになり、実力がさらに伸びることでしょう。

お近くに個別指導WAMの教室がない場合は、オンライン指導を検討してみましょう。オンライン家庭教師WAMは、個別指導WAMが培ったノウハウをオンラインで受講できるサービスです。

(4) 代々木個別指導学院

数学は、中学生それぞれの思考の癖が影響しやすい教科です。塾で数学を指導してもらう場合も、「どこまでお子さんに合わせてもらえるか」が重要。ペースや教え方、考え方がお子さんに合ってこそ、数学の力は伸びていきます。

代々木個別指導学院は、トコトン生徒に合わせられる柔軟な「キミ専用カリキュラム」が特徴。講師を含め、授業のすべてがお子さんに最適化されるため、わからなかった数学がみるみるうちに理解できるようになるでしょう。

公立高校受験はもちろん、中高一貫校に合わせた対策も可能です。めんどうみがよく、フレンドリーな講師陣と、楽しく数学を学んでいけます。

(5) ナビ個別指導学院

「数学に自信がないようだ」「やる気がなく、自分から机に向かわない」、そんな悩みをお持ちの方は、ナビ個別指導学院に相談してみませんか。ナビ個別指導学院は、お子さんを褒めて承認し、勉強へのモチベーションを上げる指導に長けた塾です。「褒め研修」を受けた講師が、お子さんの小さな努力や成果もつぶさに見つけ、やる気を引き出してくれます。

ナビ個別指導学院の授業は、基本的に学校を先取りするペースで進みます。独自開発の専用教材「ナビスタ！」を使うため、初めての単元でも無理なく習得できるのが強み。学校の授業が復習になり、「わかる」「できる」実感が育っていきます。

ナビ個別指導学院の体験授業は、たっぷり4回分。お子さんに合うか、じっくり見極めてから入塾を判断できます。

まとめ

中2数学で習う単元の内容について解説しました。

中2数学は中1の内容をふまえつつ、中3数学へつながる重要な内容ばかりです。わからないところが出てきたら、苦手意識ができる前に早めに塾などを利用し、対策することをおすすめします。

「塾探しの窓口」を使うとお子様の学習状況、性格やスケジュールに合った塾がエリアごとに探せます。上手に利用してお子様の数学の学習にお役立てください。

【中学生】数学に定評あるおすすめ塾15選｜選び方も解説

中学生に苦手教科を尋ねると、筆頭に挙げられるのが数学です。さまざまな調査でも、数学は「苦手教科ナンバーワン」の不名誉…

詳しく読む

【中学生向け】おすすめの個別指導塾15選！編集部が厳選

定期テストの点数を見て「うちもそろそろ塾が必要かな？」とお悩みでしょうか。高校受験に向けて勉強して欲しいと思う一方で、…

詳しく読む

【高校受験】勉強はいつから始めれば間に合う？元教員が解説

お子さんが高校受験を控え、 ・一般的に受験勉強を始める時期はいつ頃が多いのか・受験勉強は、間に合う（＝合格する）た…

詳しく読む