学習塾の口コミ比較サイト「塾探しの窓口」が運営。初めて塾を探されている保護者に向けて、塾を探す上での基礎知識や塾選びを成功に導くためのポイント等を、わかりやすくお届けします。
【中3数学】三平方の定理とは?三辺の比のパターンと例題・定理を解説

三平方の定理は、中3の最後に登場する単元です。高校受験が日に日に近づき、入試対策も佳境、慌ただしさが増すタイミングで習うため、学習が不十分になりやすい単元です。
しかし、高校入試では三平方の定理を使う問題は頻出。高校合格のためには、三平方の定理の確実な理解と定着が欠かせません。
この記事では三平方の定理について、基本知識や覚えておくと便利なパターン、三平方の定理を使った問題・定理を解説します。
頻出の問題パターンを中心にわかりやすくまとめましたので、入試直前の特訓に活用してください。
三平方の定理(ピタゴラスの定理)とは

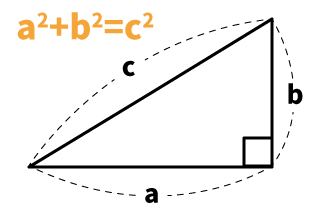
三平方の定理とは、直角三角形における3つの辺の長さの関係を公式の形に表したものです。
・隣りあう2辺の長さをそれぞれa、b
・直角の向かいにある斜辺の長さをc
とするとき、a²+b²=c²が成り立つ。
三平方の定理は「ピタゴラスの定理」とも呼ばれます。古代ギリシアの数学者であったピタゴラスが、古代バビロニアからこの定理を持ち帰り、世界で初めて証明したためにその名がつけられました。
とても美しい公式としてまたたく間に知られるようになり、現代までに数百通りともいわれる「証明」がなされているといいます。「最も多くの証明方法が知られている定理」として、ギネスに登録されたとのうわさもあります。
三平方の定理の問題が難しい理由

三平方の定理を使う問題は、一般的に「難しい」とされます。なぜでしょうか。問題の解き方にもつながる、3つのポイントを解説します。
(1) 他の単元と融合問題になりやすい
三平方の定理を使う問題には、2つのパターンがあります。
・シンプルに、1辺の長さを計算させる問題
・他の単元と融合した問題
シンプルな問題は、高校受験の第1問で登場しそうなタイプです。公式を知っていれば解けるため、困ることはないでしょう。
押さえておきたいのは、2番目です。三平方の定理は一次関数や二次関数、図形の合同・相似、さらには図形と関数を組み合わせた融合問題などにも登場します。それぞれの単元をしっかりと理解し、習熟していなければ解けない問題も多々見られます。
こうした融合問題の多さが、三平方の定理は難しいとの印象につながるのでしょう。三平方の定理の学習中に他の単元に不安を感じたら、しっかり復習しておきましょう。
(2) そもそも「三平方を使う」ことを、自分で気づけないといけない
三平方の定理を使う問題は、問題文中に「三平方の定理を使って」とはかかれません。三平方の定理を使うアプローチに、自分の力で気づく必要があります。
この「アプローチを決める」ことを、数学の世界では「方針を決める」といい、とても重要なプロセスとされます。方針を自分で見出すには、これまでの範囲を十分に理解し、使いこなせなければなりません。同時に、「この方法かな」「それとも、このやり方かな」と、知っている知識を総動員して試行錯誤できる力も求められます。
状況を自分で整理し、方針を決める過程が苦手な中学生は、総じて数学全体に苦手意識を持ちやすいようです。三平方の定理で悩んだら、「自分で気づく」ことができているか、振り返ってみてください。力不足を感じたら、早めに塾のサポートを頼ることをおすすめします。
(3) 図形の知識、観察力が必要
受験レベルの問題になると、問題の状況を踏まえ、自分で隠された角度や長さを求める必要性が出てきます。これまで学んだ図形の知識を総動員しなければならず、習熟度が足りないと、ヒントすら見つけられなくなるでしょう。
特別な直角三角形(30°・60°・90°など)、二等辺直角三角形の辺の比(1:1:√2)など、知っているかどうかで、問題を解けるかが決まるポイントもあります。
方程式や関数を優先し、図形の復習が十分でない中学生は知識や観察経験が不足し、困惑する状況になってしまいます。いまからでも遅くはありません。図形分野を中1から復習してみてください。
三平方の定理を使った基本の解き方|2つの例題

三平方の定理は、図形分野(三角形)と二次方程式を同時に使って考えます。異なる分野の知識を使いこなす必要があるため、わからなくなったり苦手になったりしやすい単元です。
まず、シンプルな問題を繰り返し解きましょう。三平方の定理に慣れたら、徐々に取り組む問題のレベルを上げていけばOKです。
例題を見ながら、三平方の定理の使い方を理解していきます。
| 【例題1】 図のxの長さを求めよ。 |
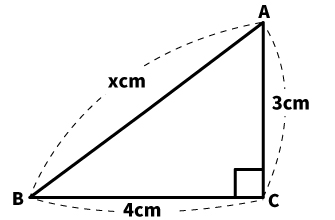
もっとも基本的な三平方の定理を使った問題です。直角三角形である点に注目し、三平方の定理を素直に使って解きましょう。
三平方の定理は、
(斜辺の長さ)2=(他の1辺の長さ)2+(もう1辺の長さ)2
です。
したがって、
x2=42+32
x2=16+9
x2=25
x=±5
三角形の辺の長さは0より大きいため、
x=5
答え x=5
もう1題、解いてみましょう。
| 【例題2】 図のxの長さを求めよ。 |
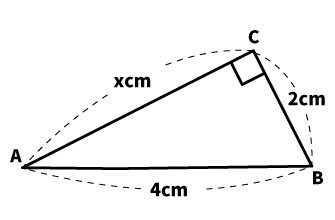
斜辺ではない辺が、xと置かれているパターンです。この手の問題は、高校入試第1問の小問として出題される場合があります。
解き方をマスターし、得点源にしてしまいましょう。
まず、三平方の定理に図の値をそれぞれあてはめます。
42=22+x2
この二次方程式を解いていきましょう。
16=4+ x2
x2=12
x=±√12
x=±2√3
x>0なので、
x=2√3
答え x=2√3
【覚えておきたい】三平方の定理・7つのパターン

三平方の定理は2乗の計算が入るため、数字が大きくなると計算に手間取ってしまいます。少しでも時間を節約したいテストや高校入試では、できるだけ計算はスピーディーに済ませたいですよね。
そこで、よく出る・よく使う、また覚えておくと便利な7つのパターンを紹介します。
三平方の定理は三角形の辺の長さの組み合わせを表す公式ですが、同時に3つの数字の組み合わせでもあります。
公式を成り立たせる数字の組み合わせを直角三角形の形とともに覚え、三平方の定理の計算スピードをグンと向上させましょう。語呂合わせなどの便利な覚え方も紹介していますので参考にしてください。
(1) 3:4:5
三平方の定理でもっともよく出るのは「3:4:5」です。本当に成立するのか、公式に代入して確認してみましょう。
三平方の定理a² + b² = c²に代入し、
3²+4²=5²
9+16=25
見事、成立しました。
辺の比が3:4:5で表される三角形は、以下の形になります。
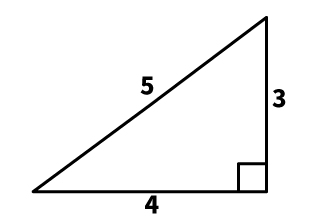
(2) 5:12:13
少し数字が大きくなりますが、「5:12:13」も三平方の定理を成り立たせる組み合わせです。
5²+12²=13²
25+144=169
5:12:13で表わされる三角形の形は、次のとおりです。
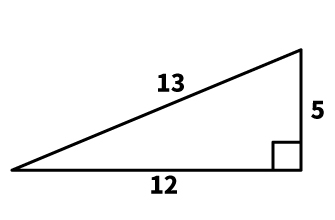
覚えにくいときは、語呂合わせで暗記しましょう。
| 【語呂合わせ】 5:12:13 (こ)(いつ)がに(いさん)⇒ コイツが兄さん |
(3) 8:15:17
もう1つ、頑張って覚えましょう!「8:15:17」も三平方の定理を成立させる数字の組み合わせです。
一見、何の脈絡もなさそうな数字の組み合わせですが、本当に成り立つのでしょうか?
8²+15²=17²
64+225=289
成り立ちました。
8:15:17で表わされる三角形の形は、次のとおりです。
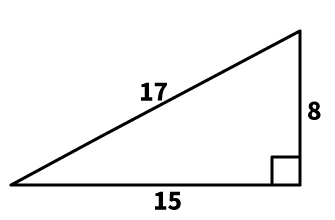
| 【語呂合わせ】 8:15:17 (は)(いご)で(じゅうなん)たいそう⇒背後で柔軟体操 |
(4) 7:24:25
整数の組み合わせは、これが最後です。「7:24:25」を見てみましょう。
7²+24²=25²
49+576=625
ここまで数字が大きくなると、確かに暗記しておいた方が計算は速く進みそうです。
7:24:25で表される三角形は、細長い形になります。
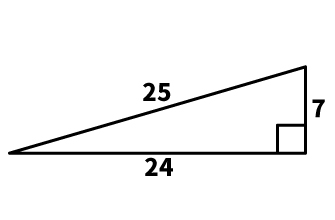
| 【語呂合わせ】 7:24:25 (な)(つ)の(よ)に(つ)め(ご)⇒夏の夜に詰碁 |
(5) 1:1:√2
数字の組み合わせは、残り3つです。ここからは「√(平方根)」が登場します。
まず、絶対に覚えておきたい組み合わせ「1:1:√2」を押さえましょう。
1²+1²=(√2)²
1+1=2
1:1:√2で表される三角形は、以下の形になります。
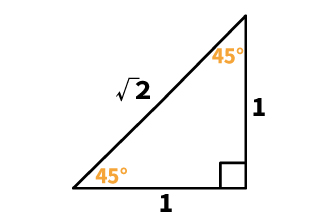
直角以外の2つの角がそれぞれ45°になるのも特徴です。三角定規セットの中にある「直角二等辺三角形」が該当します。
この角度を使った問題もよく出題されますから、しっかり覚えておきましょう。
(6) 1:2:√3
「1:2:√3」も覚えておきたい組み合わせです。三角定規セットにある、もう1つの三角定規が該当します。
1:2:√3はこれまで紹介した組み合わせと異なり、真ん中の「2」が斜辺である点に注意しましょう。
つまり、
1²+(√3)²=2²
です。計算すると、
1+3=4
確かに成立しました。
1:2:√3で表される三角形の形は、以下の図のとおりです。
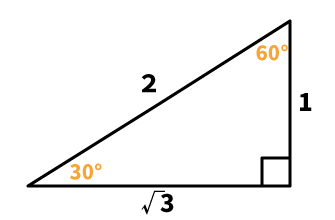
この三角形では、直角以外の2つの角がそれぞれ「30°」「60°」になります。図形問題を解く際に生きる知識なので、位置を含めてしっかり暗記しましょう。
(7) 1:2:√5
三平方の定理を成立させる数字の組み合わせも、これが最後です。最後に紹介するのは「1:2:√5」です。
1²+2²=(√5)²
1+4=5
確かに成立しました。
1:2:√5で表される三角形は、以下の形になります。
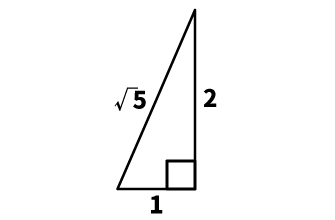
三平方の典型問題をマスターしよう<基本編>

三平方の定理を使う問題には、いくつかの典型パターンがあります。ここからは基本レベル・高校入試レベルに分けて典型問題の解き方を学びましょう。
ここでは基本レベルの問題を解説します。基本レベルの三平方の定理の問題は、次の3パターンに分けられます。
・直角三角形の一辺がわからないパターン
・直角三角形の2辺がわからず、角度がわかるパターン
・辺の長さから直角三角形かどうか見極めるパターン
順に解き方と、解法のポイントを見ていきましょう。
(1) 直角三角形の一辺がわからないパターン
直角三角形の一辺が分からない問題は、もっとも基本のパターンです。
| 【例題】 下の三角形のxの長さを求めよ。 |
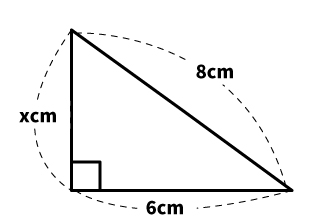
直角三角形であり、2辺の値が分かっていることから三平方の定理で解けると目途を立てます。
三平方の定理に、図の値を当てはめましょう。
x²+6²=8²
x²+36=64
x²=28
x=±√28
x=±2√7
x>0であるから、
x=2√7
答え x=2√7
また求める値は「x>0」です。マイナスを付けたり、±のまま解答したりしないよう気を付けてください。
(2) 直角三角形の2辺がわからず、角度がわかるパターン
三角形の辺の長さのうち、2辺が分からない問題もあります。このパターンでは1つの角度が与えられるため、角度をヒントに解き進めましょう。
| 【例題】 下の三角形のxの長さを求めよ。 |
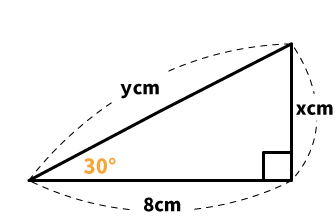
2つの辺がわからないので、このまま三平方の定理に入れても解けません。ただし、1つの角度が30°と分かっている点に注目します。
直角三角形で、2つの角の大きさは90°・30°という条件より、残りの角は60°と分かります。
さて、30°・60°・90°という角を示す三角形の辺の比を、先ほど暗記しませんでしたか?
そうです、「1:2:√3」ですね。
辺の長さの比が分かれば、x,yそれぞれを求められます。
対応する辺を間違えないように当てはめましょう。
x:y:8=1:2:√3
ここから、xとyに分けて解いていきます。
x:8=1:√3
√3x=8
x=8/√3
つまり、x=8√3/3 ・・・①
続いてyを求めます。
y:8=2:√3
√3y=16
y=16/√3
つまり、y=16√3/3 ・・・②
①②より、
答え x=8√3/3、y=16√3/3
(3) 辺の長さから直角三角形かどうか見極めるパターン
3つの辺の長さだけが与えられ、それぞれが直角三角形かどうかを問う問題も頻出です。与えられた辺の長さで実際に描いてみるわけにもいかず、辺の長さをヒントに解かなければなりません。
| 【例題】 次の3辺で表される三角形のうち、直角三角形になるものはどれか。 1. √3cm、2√2 cm、√11 cm 2. 6 cm、10.5 cm、12.5 cm 3. 12 cm、12 cm、17 cm |
この問題は「三平方の定理の逆」を使って考えます。つまり3つの数字の組み合わせが「a²+b²=c²」を成り立たせるとき、それは直角三角形であるといえる、ということです。
辺の組み合わせのうち、最も長い1つが斜辺(c)になる点に注意して計算してみましょう。
1. √3cm、2√2 cm、√11 cm
もっとも長い辺は√11。よって√11を斜辺(c)とし、残りの2辺をそれぞれa、bとして三平方の定理(a²+b²=c²)にあてはめます。
計算した結果が成立すれば、この三角形は直角三角形といえるということです。
計算してみましょう。
(√3)²+(2√2)²=(√11)²
3+8=11
式が成立しているため、この三角形は直角三角形です。
2. 6 cm、10.5 cm、12.5 cm
1と同じように考えます。もっとも長い辺は12.5cmですから、これを斜辺(c)としましょう。三平方の定理にあてはめると、
6²+(10.5)²=(12.5)²
36+110.25=156.25
左辺は146.25、右辺は156.25と式が成立しません。
よって、この三角形は直角三角形ではないとわかります。
3. 12 cm、12 cm、17 cm
もっとも長い辺は17cmです。よって17cmをcとして三平方の定理にあてはめてみましょう。
12+12=17
144+144=289
左辺は288、右辺は289と、惜しくも式が成立しません。
よって、この三角形も直角三角形ではないとわかります。
答え 直角三角形になるのは1
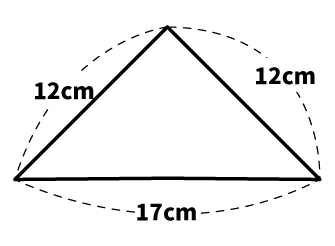
たとえば「3. 12 cm、12 cm、17 cm」の図は、以下のようになります。
図だけ見ると直角三角形のように見えますが、実は直角三角形ではありませんでしたね。
図で示される問題も見た目だけで判断せず、かならず計算して確かめる姿勢がミスを防ぎます。
三平方の典型問題をマスターしよう<高校入試レベル編>

高校入試レベルの問題は、これまで紹介してきた問題のように「数字を三平方の定理にあてはめれば解ける」とは限りません。三平方の定理の性質を踏まえ、どのように活用すれば解を求められるのか思考が必要になります。
ここでは高校入試でよく出る三平方の定理を利用した問題を、2パターン紹介します。
(1) 自分で直角三角形を作って解くパターン
直角のない三角形を与えられ、辺の長さを求めさせる問題の解き方を解説します。
| 【問題】 下の図の三角形における、xの長さを求めよ。 |
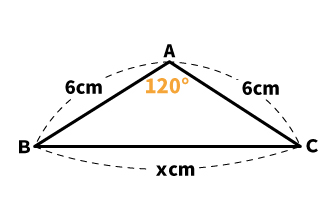
図の三角形には、直角がありません。一見、三平方の定理が使えないように見えます。
しかし、この問題は三平方の定理で解けます。
頂点aから辺bcに垂線を下ろしてみてください。すると、下の図のようになります。
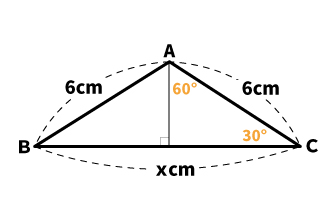
∠BACは二等分されるため、∠DACは60°になります。
60°、90°とくれば、残りの∠ACBは30°です。
3つの角がそれぞれ30°・60°・90°の直角三角形の辺の比は、いくつだったでしょうか?
そうですね、1:2:√3です。
あてはめて計算しましょう。
CA:CD=2:√3
6:CD=2:√3
2CD=6√3
CD=3√3
求めるべきx(辺BC)は2×CDなので、
答え x=6√3
(2)紙を折り返してできた三角形の面積を求めるパターン
正方形や長方形の紙を折り返しで三角形をつくり、その三角形の面積を求めさせる問題もあります。
| 【問題】 下の図における△ABFの面積を求めよ。 |
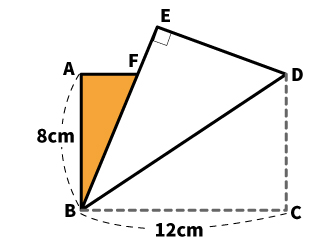
ポイントは、「長方形・正方形を折り返してできた三角形は、かならず直角三角形になる」という点です。直角三角形なら、何とかして三平方の定理で解けるのではないでしょうか。
△ABFの面積は、底辺AFの長さが分かれば求められます。AFの長さをxとし、わかる情報を図に書き込んでみましょう。
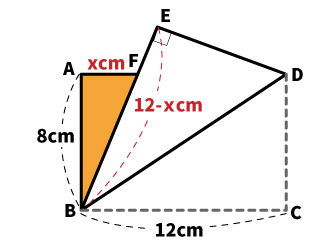
△ABFと△EDFを見てください。
AB=ED=8cm
∠FAB=∠FED=90°
さらに対頂角のため、
∠BFA=∠DFE
2つの角の大きさが等しくなったため、残りの∠ABFと∠EDFも等しくなります。
3つの角が等しいため、
△ABF≡△EDF
したがって、
BF=DF=12-x
次に、直角三角形ABFを見てください。
3つの辺の長さが出たので、三平方の定理が使えます。
x²+8²=(12-x)²
x²+64=144-24x+x²
24x=80
x=10/3
さあ、いよいよ△ABFの面積を求めましょう。
△ABF=(1/2)×(10/3)×8
=40/3cm²
答え 40/3 cm²
高校入試では三平方の定理をストレートに使わせる問題だけでなく、定理を踏まえて別の値を求めさせる問題も出ることを押さえておきましょう。
〈証明〉三平方の定理は本当に成立するのか?

「a²+b²=c²」で表される三平方の定理は、非常にシンプルな公式です。しかし、本当に成立するの?と思った人もいるかもしれませんね。三平方の定理は、実に100通り以上のアプローチで証明されています。ここではその中でも、中学生の数学で証明できる方法を2つ紹介します。
(1) 三平方の定理の証明<その1>
まず正方形を2つ使い、以下の図を描きます。
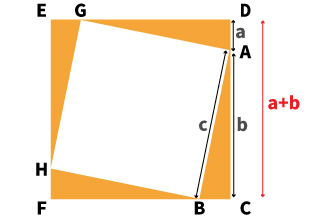
大きな正方形CDEFの中に、傾いた小さな正方形ABHGが入っています。小さな正方形の頂点ABHGは、大きな正方形に内接しています。
正方形によって生まれた直角三角形の1つ(△ABC)に注目しながら、面積を使って三平方の定理を証明していきます。
まず、△ABCの底辺をa、直角を挟んだ位置にある辺をb、斜辺をcと置きましょう。はじめに大きな正方形CDEFの面積を求めます。
大きな正方形CDEFの1辺の長さは、
a+b
と表せます。4つの三角形の辺の長さは、すべて△ABCと同じだからです。
よって正方形CDEFの面積は、
(a+b)×(a+b)=(a+b)2 ・・・①
次に、正方形CDFEの面積を「小さな正方形ABHG+直角三角形4つ分」でできていると考えます。
小さな正方形ABHGの一辺の長さはcであるから、面積は、
c2 ・・・②
と表せます。
続いて直角三角形の面積です。直角三角形の面積は、
底辺×高さ×1/2=1/2ab ・・・③
と表せました。
ここまでの式を、まとめてみましょう。
大きな正方形CDEFの面積(①)=小さな正方形ABHGの面積(②)+直角三角形4つ分の面積(③×4)ですから、
(a+b)2=c2+4×1/2ab
a2+2ab+b2=c2+2ab
a2+b2=c2
よって、三平方の定理が証明できました。
(2) 三平方の定理の証明<その2>
三平方の定理は、中3で習う「相似」を使っても証明できます。三角形の相似を使った証明方法を見てみましょう。
まず、次のような図を描きます。
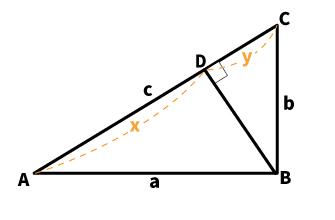
直角三角形ABCを描き、頂点Bから垂線を下ろし、交点をDとしておきましょう。
また辺の長さは、AD=x、DC=y とします。
さて、この図をみて「相似な三角形」を見つけられますか?実は、相似な三角形は3個隠れています。
| ◎ 相似1. △ABCと△ADB ∠ABC = ∠ADB = 90°・・・① ∠CAB = ∠BAD(共通)・・・② ①②より、2組の角がそれぞれ等しいので △ABC∽△ADB |
★ △ABC∽△ADBなので、対応する辺の比も等しくなります。
c : a = a : x
a² = cx ・・・③
| ◎ 相似2. △ABCと△BDC ∠ABC = ∠BDC = 90°・・・④ ∠CAB = ∠BAD(共通)・・・⑤ ④⑤より、2組の角がそれぞれ等しいので △ABC∽△BDC |
★ △ABC∽△BDCも、対応する辺の比が等しいですね。
c : b = b : y
b² = cy ・・・⑥
さて、相似な三角形から導かれた③と⑥に注目してください。
③+⑥を計算すると、
a² + b² = cx + cy
a² + b² = c (x + y)
a² + b² = c²
こちらも、三平方の定理が証明できました。
三平方の定理の証明は、ほかにもさまざまあります。興味がわいたら、ぜひ調べてみてください。
三平方の定理を習得する4つのコツ

三平方の定理は中3の最後に習う割に高校入試での出題頻度が高く、失点の原因になるケースがよく見られます。
高校入試本番までに十分理解し使いこなせるよう、計画的に練習していきましょう。
ここでは三平方の定理を習得するコツを解説します。
(1) よく出る辺の比は早めに覚えてしまおう
記事でも、よく出る辺の比を7つ紹介しました。
| 【復習】 覚えておきたい直角三角形の辺の比 3:4:5 5:12:13 8:15:17 7:24:25 1:1:√2 1:2:√3 1:2:√5 |
これらは、できるだけ早く覚えることで、後の問題演習が楽になります。
とくに、最優先で覚えたいのは「3:4:5」「1:1:√2」「1:2:√3」の3つです。その上で「5:12:13」「1:2:√5」を覚える順番にすると、無理なく効率的に学習が進みます。
(2) 典型パターンの問題を繰り返そう
三平方の定理は、先に紹介したようにいくつかの典型的なパターンに分けられます。まずは典型パターンの問題を繰り返し、解き方を身につけましょう。
また「3:4:5」「1:1:√2」「1:2:√3」など、覚えた辺の比は問題演習の中で積極的に使います。知識は使うことで自分のものになり、さまざまな応用に利用できるようになります。
学校の問題集や入試の過去問を利用して、さまざまな問題に取り組んでみてください。
(3) 補助線を積極的に引こう
三平方を利用した図形問題は、補助線を引くことで解答の方針が立つものもあります。図を見たら積極的に補助線を書き込み、ヒントを探すようにしましょう。
とくに「垂線は直角をつくる」という定理は大切です。直角があれば三平方の定理を使える可能性が高まります。垂線にも注目してみてください。
(4) 塾や家庭教師の力も借りる
入試直前は、三平方の定理だけに掛かりきりになってはいられません。他の単元も英語も国語も、勉強したいことが山ほどあるはずです。
そんな忙しい入試直前期に登場する三平方の定理は、塾や家庭教師の力を借りて効率的にマスターするのがおすすめです。プロならではのポイントを押さえた解説で、一気に理解が進み問題が解けるようになります。
【中3数学】重要単元を効率良く復習する方法

三平方の定理を得点源にするためには、他の単元の習得も欠かせません。とくに計算と関数、図形の既習範囲は、三平方の定理と融合しやすく、最優先で復習しておきたいところ。
忙しい中3生が効率良く復習する方法を紹介します。
(1) 苦手・理解不足の単元を発見する
まずは、どこが苦手なのか、理解が不足している単元はどれかを見極めます。この見極めによって、単元ごとの復習の優先順位が決まります。
ワークや問題集の章末にある、「まとめ問題」「実力テスト」といったページを利用しましょう。既習範囲からまんべんなく出題されているページです。このページを解き、以下に該当する単元が、優先的に復習したいところです。
〈最優先で復習〉
・まったく手が出ない
・なんとなく記憶はあるが、解き進められない
〈次に復習〉
・手は動いたが、解法が正解と異なる
・1つ~2つの知識不足があり、解き切れなかった
(2) 基本問題を3周する
優先的に復習すべき単元がわかったら、基本問題からやり直します。まずは3周を目標に、「何も見なくても解き、正解できる状態」をめざしましょう。
最初は、解説を見ながらでも構いません。正しい解き方や考え方をインプットし、納得しながら進めます。
この段階で分からない箇所があれば、学校の先生に質問する・塾を利用するといった第三者のサポートが必要になります。
(3) スキマ時間を活用する
ある程度、復習が進んでくると、1問にかかる時間が短くなります。机に向かっての復習から、スキマ時間での確認に移行していきましょう。
復習した箇所をスキマ時間で確認できるようになると、机に向かう時間にまた別の復習等に取り組めるようになります。勉強できる範囲がどんどん広がり、得点力も伸びていくでしょう。
【中3数学】三平方の定理や受験勉強指導に強い塾5選

三平方の定理をはじめ、数学の他単元も、さらに英語に国語、理科社会と、高校合格には5教科の総合力を高める対策が欠かせません。一人ひとり異なる苦手や、学習ペースに合わせたサポートを受けるなら、個別指導塾がおすすめです。
高校受験に向けた対策に定評ある個別指導塾を、厳選して5つ紹介します。
個別教室のトライ
個別教室のトライは、すべての授業をマンツーマンで行う塾です。マンツーマン指導の良さは、授業のすみずみまで中学生に合わせられること。三平方の定理に欠かせない要素、たとえば平方根の計算に理解不足が見られれば、さかのぼっての計算トレーニングも自在です。
個別教室のトライで指導する講師は、誰もが十分な指導力と教科知識を持っています。高校受験で問われやすいポイントを踏まえた指導や、苦手を克服し得点源にする学習法なども教えてもらえます。
お近くに個別教室のトライがない中学生、あるいは自宅で集中的に取り組みたい中学生には、トライのオンライン個別指導塾がおすすめ。トライ品質の授業をオンラインで受講できるサービスで、自宅でマンツーマン指導を受けられます。
個別教室のトライの料金情報は、以下のとおりです。
| 入会金 | 11,000円 |
| 中学生授業料 | 26,000円~30,000円/月 |
| その他費用 | 季節講習費 35,000円~70,000円 |
※ 授業料は120分の授業を月4回受講した場合の費用目安
最短1分で完了! 個別教室のトライのお近くの教室に無料資料請求する
東京個別指導学院・関西個別指導学院
東京個別指導学院・関西個別指導学院は、中学生の理解度や習熟度に合わせた指導を得意とする塾です。授業スタイルは、講師1人が生徒2人を担当する1対2。生徒に合わせた解説をマンツーマンで実施した直後に、該当単元の問題演習に取り組めるため、理解と定着が最適なペースで進みます。
東京個別指導学院・関西個別指導学院が個別に策定する学習計画は、苦手単元の重点取り組みも要望可能。基礎計算に不安がある、数学が全体的に苦手など、どのような悩みも相談してみてください。
ベネッセグループの塾として、高校受験情報も豊富に持っています。志望校に関する情報、対策の進め方、出願の戦略など、進路相談でも頼りになる存在です。
東京個別指導学院・関西個別指導学院の料金情報は、以下のとおりです。
| 入会金 | 0円 |
| 中学生授業料 | 受講教科や回数、ペース、使用教材などによって変動 要問合せ |
| その他費用 | 設備費(月々3,960円) 季節講習あり |
無料資料請求する 最短1分で完了! 関西個別指導学院のお近くの教室に
無料資料請求する
個別指導WAM
個別指導WAMは、中学生一人ひとりに合わせ、テスト・受験の成績を上げることを目標とした指導を実践します。地域の中学校や高校情報に精通しており、学校別の傾向に合わせた対策が得意。指導力の自信は、中学生向けに実施する「成績保証制度」となってあらわれています。
※ 成績保証制度:入塾後、一定期間内の定期テストで1教科+20点以上、もしくは80点以上達成を約束する制度。詳しくは個別指導WAMにお問い合わせください。
指導する講師陣の力量も、ピカイチです。難関大生やプロ講師を中心とした講師が、三平方の定理の考え方から丁寧に解説します。
個別指導WAMと変わらぬ品質の授業をオンラインで受けられるオンライン家庭教師WAMも、人気のサービスです。自宅で受講でき、自分に合ったペースの学習が実現します。
個別指導WAMの料金情報は、以下のとおりです。
| 入会金 | 入会金、登録費用、年会費が必要 金額は要問合せ |
| 中学生授業料 | 中1 7,600円~ 中2 7,600円~ 中3 8,400円~ |
| その他費用 | 維持管理費、e-ラーニング教材費 季節講習あり |
※ 授業料は週1回・40分コースを受講した場合の月額
最短1分で完了! 個別指導WAMのお近くの教室に無料資料請求する
代々木個別指導学院
代々木個別指導学院は、熱意と指導力あふれる講師が評判の塾です。中学生一人ひとりに合わせ柔軟に対応する授業で、三平方の定理がみるみるうちに理解できるはず。論理的思考力や情報整理力が必要な三平方の定理の証明も、自信を持って自分の力で完成させられるようになるでしょう。
「キミ専用カリキュラム」と呼ばれる、カスタマイズ性の高い授業計画も魅力の1つ。苦手の根本原因を発見し、さかのぼって徹底的に克服する「リターン学習法」など、さまざまな独自の学習メソッドも丁寧に教えてもらえます。
代々木個別指導学院の料金情報は、以下のとおりです。
| 入会金 | 20,000円 |
| 中学生授業料 | 10,800円~ |
| その他費用 | 管理料・諸経費 季節講習 30,000円~40,000円 |
※ 授業料は週1回・1教科を受講した場合の月額
最短1分で完了! 代々木個別指導学院のお近くの教室に無料資料請求する
ナビ個別指導学院
ナビ個別指導学院は、「褒める指導」を軸とし、自分でできる状態にまで力強く導く塾です。褒めスキルを伸ばす研修を受けた講師が、中学生のちょっとした成長もつぶさに発見して、承認。塾に行くたびに努力が認められる実感を得られ、勉強へのやる気が倍増します。
テストや受験の本番、自分一人の力で問題を解ききり、目標点を取れる状態にするために、本質的な理解と実戦力を伸ばす指導もナビ個別指導学院の特徴。勉強が成果につながる喜びが得られ、次の頑張りの原動力になる良いサイクルが回り始めるでしょう。
ナビ個別指導学院の料金情報は、以下のとおりです。
| 入会金 | 22,000円 |
| 中学生授業料 | 中1~中2 12,600円 中3 16,800円 |
| その他費用 | 季節講習 コマ単価 3,700円 諸経費 3,480円(月額) |
※ 授業料は週1回受講した場合の月額料金
最短1分で完了! ナビ個別指導学院のお近くの教室に無料資料請求する
まとめ
三平方の定理は「定理の理解」と、理解した知識を使っての「練習」が成果を作る単元です。まずどうして定理が成立するのか、しっかり理解しましょう。その上で問題演習に取り組むと、スムーズに進めます。
またわからない問題に当たったら、きちんと解決しておくことも大切です。入試でも三平方の定理は頻出です。直前に「わからない」と放置した問題が、入試に出るかもしれません。
学校の先生、あるいは塾や家庭教師に質問し、納得できるまで取り組みましょう。しつこくくいさがる貪欲さが、合格につながります。
お子さんに合う塾や家庭教師を見つけるには、「塾探しの窓口」をご利用ください。学年とお住まいの地域を入力するだけで、地域の「本当に評判の良い塾」を見つけられます。



中学生向けのおすすめ塾
中学生向けの塾の料金・口コミ
- 個別教室のトライの料金・口コミ
- 東京個別指導学院・関西個別指導学院の料金・口コミ
- 代々木個別指導学院の料金・口コミ
- 個別指導WAMの料金・口コミ
- ナビ個別指導学院の料金・口コミ
- 中高一貫校専門 個別指導塾WAYSの料金・口コミ
- スタディコーチの料金・口コミ
- 坪田塾の料金・口コミ
- 個別指導塾トライプラスの料金・口コミ
- 個別指導学院サクシードの料金・口コミ
- 個別指導スクールIEの料金・口コミ
- 個別指導塾スタンダードの料金・口コミ
- 個別指導塾サクラサクセスの料金・口コミ
- ドリームホームスクールの料金・口コミ
- みやび個別指導学院の料金・口コミ
- ITTO個別指導学院の料金・口コミ
- コノ塾の料金・口コミ
- 学習空間の料金・口コミ
- キズキ共育塾の料金・口コミ
- 森塾の料金・口コミ
- 自立学習REDの料金・口コミ