学習塾の口コミ比較サイト「塾探しの窓口」が運営。初めて塾を探されている保護者に向けて、塾を探す上での基礎知識や塾選びを成功に導くためのポイント等を、わかりやすくお届けします。
【中2数学】連立方程式の計算方法と文章問題の解き方のコツを分かりやすく解説

連立方程式は中学数学で学ぶ方程式の一つで、高校入試でも頻出の単元です。求める解が2つ(問題によっては3つ以上)に増えることから、苦手とする中学生が多くなります。
しかし解き方を理解してしまえば、定期テストや高校入試では得点源にできる単元でもあります。
この記事では中2で学ぶ連立方程式の解き方、代表的な例題の立式の仕方を解説します。あわせて、連立方程式や数学全般の対策におすすめの塾も5つ紹介しています。この記事を参考に、連立方程式を得意単元にしてください。
今すぐおすすめの塾を知りたい方へ連立方程式や数学全般の対策におすすめの塾5選はこちら
連立方程式とは

中1では「方程式(一元一次方程式)」を習いました。中1で学んだ方程式はわからない値(求める解)は1つだけで、おおむね「x」に置き換えていたのではないでしょうか。
中2で学習する連立方程式とは、「二元一次方程式」つまり、2つ以上の文字(求める値)があるときに使われる方程式が、2つある方程式です。求める解が2つのとき、解を求めるための方程式は2つ必要です。
【例】
(1) y=x+2 という式があるとき、このxとyを満たす数字は無限にある。(x=1ならy=3、x=5ならy=7など)
(2) y=x+2, y=3x+6 と2つの方程式があると、以下のようにそれぞれの文字の値が1つに定まる。
x+2=3x+6
-2x=4
答え x=-2, y=0
★ 元:変数の種類の個数
★ 次:変数の最大の次数
変数とは値が定まっていない文字、つまりxやyです。この種類の個数を“元”といいます。また、次数とは累乗の数です。
二元一次方程式とは、変数(xやy)が2種類あり、累乗は1の方程式という意味です。まさに、連立方程式ですね。
数学では、こうした一見すると難しい用語がたくさん登場します。一つずつ意味を正しく理解し、「見た目の難しさ」に惑わされないようにしましょう。
連立方程式の解き方|加減法と代入法

連立方程式を解く方法は2つあります。
・加減法
・代入法
どちらの方法でも、2種類ある文字の一つを消してもう一つの文字だけの式にすることで解ける仕組みになっています。ここではこの2つの解法について説明します。
(1) 加減法
「加減法」は、数式を足したり(加法)、引いたり(減法)して解くため、こう呼ばれます。
連立方程式のすべての文字に係数がついている場合は、加減法で解いたほうが確実でスピ-ディ-です。とはいえ、計算ミスに注意して進めましょう。
加減法を使った連立方程式の解き方
加減法の基本手順は、次のとおりです。
| 1.連立方程式の2つの式を見比べ、係数が同じものを見つける。 係数が同じ文字がない場合は、最小公倍数を使うなどして、係数を同じにできる項を見つける。 2.2つの式を足し引きし、係数が同じ項を消し文字を1つだけにする。 3.計算して、一方の文字の解を求める。 4.出た解を使い、もう一方の文字の解を求める。 |
数式を使って解いてみましょう。
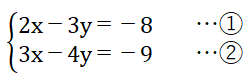
上記①の2xと②の3xのそれぞれの係数は、2と3の最小公倍数「6」にできることに気づく。(yの係数3と4の場合は最小公倍数が12のため、計算が複雑になる。よってこの場合はxの係数をそろえる方針にする)
それぞれの式に、①×3、②×2の操作を行うと、以下のようになる。
6x-9y=-24 …③
6x-8y=-18 …④
③-④を計算すると、
-y=-6 両辺に-1をかけて、
y=6 …⑤
⑤を①に代入すると、
2x-3×6=-8
2x-18=-8
2x=10
x=5
答え x=5, y=6
ただしスピ-ディ-に計算を終えるためには、できるだけ簡単に計算できる方に代入することがマストです。
「どちらに代入したほうが、より簡単に計算できるか」と見極める力も、問題を解きながら身に着けていきましょう。
(2) 代入法
代入法は2つある式の片方を、もう一方に代入して解くやり方です。「x+y=5」「y=3x-1」など、xやyに係数がない式があるときに利用します。
係数がある式でも代入法で解けないことはありませんが、計算プロセスが増えるため、計算ミスが起きやすくなります。すべての文字に係数がある場合は、上で解説した「加減法」を使ってください。
代入法を使った連立方程式の解き方
代入法の基本手順は、次のとおりです。
| 1.係数のない文字を含む式を変形し、「x=~~」「y=~~」の形にする。 2.1をもう一方の式(B)に代入し、xもしくはyの解を出す。 3.出た解を1にあてはめ、残りの文字の解を出す。 |
実際に数式を使って解いてみましょう。
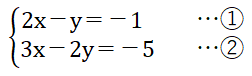
①に係数がないyがあるため、この式をy=ax+bの形に変形し、代入法で解く(方針決定)。
2x-y=-1(①)を、移項してy=ax+bの形に変形すると、
y=2x+1 …③
③を②に代入する。
3x-2(2x+1)=-5 …④
④を解く。
3x-4x-2=-5
-x=-3
x=3 …⑤
⑤で出たxの解を、③にあてはめるとyの解が出る。
y=2×3+1
y=6+1
y=7
答え x=3, y=7
連立方程式の鬼門「連立方程式の利用(文章題)」

連立方程式の計算を習得できたら、連立方程式の利用に入ります。いわゆる、文章題です。定期テストや高校入試では、連立方程式の文章題がかならずといって良いほど出題されます。
「苦手」「嫌い」という中学生も多い連立方程式の文章題ですが、実はいくつかの典型パタ-ンに分けられます。ここでは頻出の4パタ-ンを解説しますので、解き方とポイントをしっかり理解してください。
【典型パタ-ン例題1】 速さの問題
典型的な問題パタ-ンの1つめは「速さ」をテ-マにしたものです。「道のりの問題」と呼ばれることもあります。
| <問題例> 310km離れた目的地まで、車で移動する。はじめ、高速道路を時速100kmで走り、 途中から一般道に下りて時速50kmで進んだ。目的地までの所要時間は3時間30分だった。 高速道路と一般道の走った道のりをそれぞれ求めよ。 |
まず、どの要素を文字に置くか決めます。今回は「高速道路と一般道の走った道のり」を求めなければならないので、これを文字にしましょう。
・高速道路の道のりをx
・一般道の道のりをy
目的地までの道のりは310kmでした。つまり高速道路で走った道のりと一般道で走った道のりを合計すると310kmということです。
したがって、次の式が成り立ちます。
x+y=310 …①
次に、もう1つの要素である「速さ」に注目しましょう。
高速道路xkmを時速100kmで走り、一般道ykmを時速50kmで走った結果3時間30分かかったという情報から、次の式を立てられます。
x/100+y/50=3.5 …②
※ 自動車が進むスピードは「時速」であらわされています。所要時間「3時間30分」も、分ではなく時間に合わせて表示しなければ、つじつまが会いません。3時間30分を「3.5(時間)」としている点にも注目してください。30分は0.5時間ですよね。
①と②から連立方程式ができました。
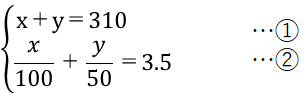
②は分数があって計算しにくいですね。両辺に100をかけ、分数ではなくしてしまいましょう。
②の両辺に100をかけると、
x+2y=350 …③
①-③を計算して、
y=40
y=40を①に代入し、
x+40=310
x=270
したがって高速道路を走った道のりは270km、一般道を走った道のりは40kmだとわかりました。
答え 高速道路 270km、一般道 40km
・道のりや速さの問題は、さまざまなパタ-ンがあります。紹介した問題は「道のり」を答えさせるものでしたが、速さや時間を答えさせる問題もあります。パタ-ンが変わると難しく感じるかもしれませんが、「文字に置く要素を見つけ」「速さと時間、距離の関係から立式する」基本手法は変わりません。さまざまな問題を解き、コツをつかんでください。
【典型パタ-ン例題2】整数の問題
「整数を題材にした問題」もよく出されます。どのような問題が該当するか、問題例を見てみましょう。
| <問題例> 2つの整数がある。大きい数の3倍と小さい数を足すと、和が6になる。 大きい数から小さい数の2倍を引くと、差が23となった。 大きい整数と小さい整数を、それぞれ求めよ。 |
ぼんやり眺めていても問題は解けません。与えられた状況を整理し、「何を文字に置くべきか」から考えていきましょう。
今回の問題では、「大きい整数と小さい整数」を求める必要があります。したがって、次のように文字に置くのが正攻法です。
・大きい整数を、x
・小さい整数を、y
文字に置く要素が決まったので、文字を使いながら問題を式にしていきます。
まず「大きい数の3倍と小さい数を足すと6」を式にすると、
3x+y=6 …①
次に「大きい数から小さい数の2倍を引くと23」を式にすると、
x-2y=23 …②
①と②で連立方程式ができました。
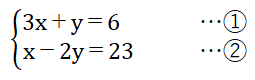
解いていきましょう。
①に係数のないyがあります。代入法で解けそうですね。
①をy=の形に変形し、
y=6-3x …③
③を②に代入し、
x-2(6-3x)=23
x-12+6x=23
7x=35
x=5
x=5を①に代入すると、
3・5+y=6
15+y=6
y=-9
x=5、y=-9 と答えが出ました。
答え 大きい整数 5、小さい整数 -9
【典型パタ-ン例題3】割合を使った食塩水の問題
「食塩」をテ-マにした問題も典型例です。小学校で習った「割合」の考え方を使う問題で、割合が苦手だった生徒はこの問題も苦手としやすいようです。
| <問題例> A、Bの2つの食塩水がある。Aは濃度が5%、Bは8%である。 AとBの食塩水を混ぜ合わせ,6%の食塩水600gをつくりたい。 A、Bそれぞれ何gずつ使えばよいか求めよ。 |
速さの問題と同じように、求める値を文字におきましょう。今回は「必要なAの食塩水(g)とBの食塩水(g)」を求めなければならないので、これを文字にします。
・Aの食塩水の量 x
・Bの食塩水の量 y
次に、状況が2つに整理できることに注目します。
1. (A・5%)+(B・8%)=6%
2. 6%の食塩水の重さは600g
どうやら連立方程式が作れそうですよ。それぞれを式にしてみましょう。
1より、
x×5/100+y×8/100=600×6/100 …①
2より、
x+y=600 …②
①の理解が厄介かもしれません。①にある「5/100」「8/100」「6/100」は、それぞれ5%、8%、6%であることを示します。%は百分率、100で割った割合であることを思い出してください。
そしてそれぞれの食塩水の量がxg、yg、600gであるため、百分率をかけています。
さあ、立式できたので①と②を連立方程式にして解いてみましょう。
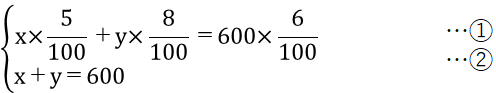
①の分数が計算しにくいので、また両辺に100をかけて分数を消します。
①の両辺に100をかけると、
5x+8y=3600 …③
②の両辺に5をかけると、
5x+5y=3000 …④
③-④を計算して、
3y=600
y=200
y=200を②に代入すると、
x+200=600
x=400
答え Aの食塩水400g、Bの食塩水200g
百分率、歩合の基本も復習しておきましょう。
【典型パタ-ン例題4】割合を使った全校生徒の増減の問題
苦手意識を克服するために、割合の典型問題をもう1題紹介します。全校生徒の増減に関する問題です。
| <問題例> ある中学校では、昨年度360人が入学した。今年の入学者数は、 昨年より男子が3%減少、女子が5%増加した。 全体では2人増加したという。昨年の男子、女子の入学者数をそれぞれ求めよ。 |
この問題も、まずは落ち着いて求めるべき値を文字に置きましょう。「昨年の男子、女子の入学者数をそれぞれ求めよ」との指示ですから、次のように置きます。
・昨年の男子の入学者数 x
・昨年の女子の入学者数 y
次に、与えられた情報を整理します。
まず、昨年度の入学者総数は360人であることがわかっていますね。したがって、次の式がつくれます。
x+y=360 …①
次に今年の入学者数を式にしますが、ここがポイントです。今年の入学者数は「男子が昨年人数(x)より3%減少」「女子が昨年人数(y)より5%増加」したとのこと。これを式にしなければなりません。
増減がなく、昨年と同人数が入学した場合の増減割合は100%、つまり100/100です。これを踏まえ「男子が3%減少」を式にするとどうなるでしょうか。
今年の男子の入学者数は、100%から3%減らして
97/100×x …②
とあらわせます。97/100とは、97%のことです。
同様に今年の女子の入学者数は、100%から5%増やして
105/100×y …③
とあらわせます。105/100とは、105%です。増えているのですから、100を超える数字になります。
さあ、②と③から式を作りましょう。
今年の入学者数は「男子が97/100×x、女子が105/100×y」で、結果的に2人増えて362人になったそうですから、
97/100×x+105/100×y=362 …④
①と④で連立方程式にします。
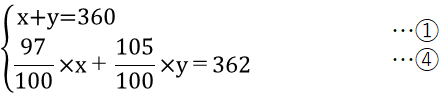
④の分数が厄介なので、両辺に100をかけて分数を外します。
97x+105y=36200 …⑤
①に105をかけ、加減法で解きましょう。
105x+105y=37800 …⑥
⑥-⑤より、
8x=1600
x=200
x=200を①に代入して、
200+y=360
y=160
答え 昨年の男子の入学者数 200人、昨年の女子の入学者数 160人
※ 200と160を足すと360になり、たしかに問題文に合致します。もし足して360にならない場合は、どこかで計算ミスをしています。見直してみてください。
【苦手理由1】複雑でミスを起こしやすい→問題演習で慣れる
連立方程式の計算は、加減法と代入法のいずれかで必ず解けます。「解き方」自体はそれほど難しくありません。連立方程式の計算が厄介なのは、「係数を合わせるために最小公倍数を探す」「出た解を元の式に代入してもう1つの文字を出す」など、途中の計算が煩雑になりやすい点です。
【対策】問題演習を繰り返し、パターンを覚えて慣れよう
基本問題・典型問題からやや難しいレベルの問題まで載っている問題集を利用し、数多くのパタ-ンを解いてみてください。計算する1行1行で「いま、何をしているのか」「何を求めたくてこの計算をしているのか」と意識しながら解くと、連立方程式の計算を徐々に理解できます。
【苦手理由2】文章題の立式が難しい→言葉を式にする練習を行う
連立方程式の文章題が難しい理由は、2つあります。
・どの要素を文字に置けばよいか迷いやすい
・要素同士の関係を式に表すのが難しい
中1で習った方程式は、問題文のなかで不明な要素(文字に置き換える要素)が1つだけでした。ところが連立方程式は、不明な要素が2つあります。
2つの要素について関係性を見出し数式にしないといけないため、考えるべき項目が多くなります。「何を文字にして式を作ればいいのか」「関係を式にするにはどうすればいいのか」と悩んでしまう中学生が大勢います。
また1つの問題文に複数の単位が登場する点も、連立方程式の文章題を難しく感じる原因です。速さの問題なら、「時間(分、時間)」「距離(km、m)」「速度(時速、分速)」と、いくつもの単位が出てきます。
それぞれの単位同士の関係が見いだせず、解けなくなる中学生もいます。
【対策】言葉を式にする練習を、簡単なものからトライしよう
連立方程式の文章題は、解く前に立式ができるかが重要です。「適切な要素を文字に置けるか」「要素の関係性を見極められるか(式に起こせるか)」で決まります。そこで、連立方程式の立式が苦手な人は、日本語を数式にする練習に取り組んでみましょう。
連立方程式が得意になる5つの勉強法

連立方程式は、正しい練習法で取り組めば得意分野にできます。まずは基本計算を、次に文章題を練習し、得点源にしましょう。
ここでは連立方程式の勉強法を5つの手順に分けて解説します。
(1) 計算は1行1行、丁寧に解く
連立方程式は、それまでの単元よりもかなり計算量が増えます。分数や小数、大きな数字を扱う問題も多いため、必然的に計算ミスが起きやすくなります。
そこで、連立方程式の計算は、1行1行を丁寧に・確実に進める意識を大切にしましょう。
連立方程式の計算ミスを減らすコツは、2つあります。
◎ 【コツ1】次の行に進んだら、直前の式と見比べる
計算過程が長くなりやすい連立方程式は、最終的な解を出してからミスに気付くと、かなり大変です。もし入試なら、時間がなくて修正ができないと合否を左右するおそれも…。早めに計算ミスに気づけるよう、1行ごとの確認を癖づけるのがおすすめです。
計算を1行進めたら、1行上の式と見比べて「おかしなところがないか」さっと確認するだけです。しかしこの一瞬の確認で、「マイナスになるべき数字がプラスのまま」「桁を書き間違えていた」などのミスに気づけるようになります。
◎ 【コツ2】ノートは贅沢に、たっぷり使う
連立方程式に限った話ではありませんが、数学の勉強は「ノートをふんだんに使う」のが大切です。
時々、ノートを“きれいに”まとめたい意図からか、途中計算やメモを余白に小さく書く生徒がいますが、それはおすすめできません。小さく書く計算は、ミスの巣窟です。マイナスを見落としたり、スペースがなくて途中計算を十分書けなかったりと、間違いにつながる原因が詰まっています。
ノートは贅沢に、たっぷり使ってください。「スペースがありすぎるかな?」くらいでちょうど良いです。
そして、途中式=解法を必ず、順を追って、きちんと書きましょう。見直しをする際も、途中式があることで自分がどこで間違えたのかがわかります。何より、正しい途中式の書き方は徹底的に守ってください。自己流は禁物です。
英語のテストで文末にピリオドが抜けていたら減点されるように、数学も、解法の書き方そのものがおかしいと採点対象とみなされません。これは、高校入試でも大学入試でも全く同じです。早い段階で身に着けておきましょう。
(2)文字に置く数字と関係性を見極める
先に解説した、連立方程式の文章題を思いだしてください。どの問題でも「どの要素を文字に置くか」「要素同士の関係性はどうなっているか」を、はじめに考えました。
繰り返しになりますが、連立方程式の文章題が解けるかどうかは、「適切な要素を文字に置けるか」「要素の関係性を見極められるか(式に起こせるか)」で決まります。
連立方程式の立式が苦手な人は、日本語を数式にする練習に取り組んでみましょう。
たとえば問題文で「合わせて」とあったら、足し算(加法)ですね。「~より」「~と比べて」とあったら割合を使います。「時速」という表現は、距離/時間で数式にできます。分速と秒速が混ざっている場合は単位をそろえなければなりません。
文章題が苦手な中学生は、日本語と数式の転換がうまくいかないケースが多く見られます。ごく簡単な文章題から、日本語と数式の転換練習をしてみてください。日本語から数式への転換がうまくできない場合は、線分図や図を書いてみる手法がおすすめです。状況を視覚的に理解しやすくなり、式に転換できる部分を見つけられるはずです。
(3) 「等式である」事実に目を向ける
方程式の立式が苦手な生徒の多くが見落としているポイントは、「方程式は等式である」事実です。
等式とは、「AとBが等しい」ことを式にしたものです。イコールでつながれた左右は、同じものを指します。難しいのは、右と左が、同じように事象を見ているわけではない点でしょう。
先に紹介した「速さ」の典型問題に、以下のような記述がありました。
| 310km離れた目的地まで、車で移動する。はじめ、高速道路を時速100kmで走り、 途中から一般道に下りて時速50kmで進んだ。 |
この部分を、解説では以下のように立式しています。
高速道路の道のりをx、一般道の道のりをyとして、
x+y=310
左辺は、高速道路と一般道の道のりを、それぞれ別個に見ています。右辺では、この人が走行した総距離を見ています。実体験に置き換えると、この両者を「同一のもの」と考えるのは、なかなか難しいもの。イコールでつなげて考える段階で、1つハードルがあるのです。
つまり、等式である方程式を立式する際は、「何と何が同じなのか」に注目する意識が重要になります。ここが、連立方程式の最大の関門かもしれません。 自力での練習が難しい場合、あるいは自分の考え方が正しいか分からない場合は、早めに塾のサポートを頼ってください。
(4) 典型パタ-ンの問題を中心に演習する
要素を文字に置けて、数式を立てられるようになったら、典型パターンの問題を繰り返し演習します。高校入試で出題されるハイレベルな問題も、実は典型パターンや基礎の組み合わせでできていることが多いものです。典型パターンをマスターすれば、解ける問題のバリエーションが相当に増えるでしょう。
定期テスト対策におすすめの教材は、学校から配布されているワークや問題集です。「A問題」「基本問題」とされる問題は、連立方程式の文章題を解くために必要な力がつく、典型問題で構成されています。
まず「A問題」「基本問題」を何も見ずに完答できる状態を目指しましょう。「A問題」「基本問題」ができるようになったら、次は「発展問題」へとレベルアップしていきます。
高校入試対策には、全国の入試過去問を集めた「全国高校入試問題集」がおすすめです。市販されていますので、書店などでチェックしてみてください。
(5) どうしてもわからなければ、塾や家庭教師の力も借りる
連立方程式の文章題を解くキーポイントである、「適切な要素を文字に置けるか」「要素の関係性を正しく式に起こせるか」をマスターするのは、一人で習得するのは実は簡単ではありません。
正しく式に起こすためには、割合や速さ、整数など、これまで習った単元の正しい理解が不可欠なためです。これらの理解があいまいなまま、連立方程式をマスターしようとしても頓挫してしまうでしょう。
連立方程式の習得と過去の単元の復習を効率良く進めるには、プロの手を借りるのが近道です。塾や家庭教師のサポートを受けながら、弱点を補強しましょう。理解不足があった単元をマスターできると、連立方程式もスムーズに解けるようになります。
身近なところにある連立方程式の例

連立方程式に限らず、数学の文章題は場面設定が現実離れしているものが多々あります。「こんなこと、ありえないでしょう」「普通、こんなことしないよね」と、設定を受け入れられず、思考が進まない経験は、誰しもあるものです。
ただ、連立方程式は、私たちの生活のいたるところに潜んでいます。連立方程式が身近になる場面を2つ、紹介します。文章題の場面設定に拒否感を抱く場合は、より現実的な問題から挑戦してみてください。
(1) ファーストフード店で買い物
ファーストフード店で、ハンバーガーとジュースを買うシチュエーションを考えてみましょう。
M店では、ハンバーガーを3個とジュースを1つ買うと750円になるセットを売っています。また、ハンバーガー1個とジュース1つを買うと、350円になるそうです。
どちらのハンバーガー・ジュースも、同じ商品です。さて、ハンバーガーとジュースは、それぞれいくらでしょうか。
*****
この問題では、未知の数がハンバーガー1個の値段と、ジュース1つの値段です。ハンバーガー1個の値段を x 円、ジュース1つの値段を y 円として、立式します。
ハンバーガーを3個買うと750円になるのですから、
3x+y=750 ・・・①
ハンバーガー1個とジュース1つを買うと350円になるのですから、
x+y=350 ・・・②
①と②を連立させて解くと、
(x,y)=(200,150)
したがって、ハンバーガーは200円、ジュースは150円です。
(2) 遊園地で入場チケットを買う
2つの家族が遊園地に行きました。入園料は、それぞれ以下のようにかかったそうです。
・大人4人+子ども3人の家族は、合計18,000 円
・大人2人+子ども2人の家族は、合計10,000 円
さて、この遊園地の入場チケット、大人・子どもそれぞれいくらでしょうか?
*****
未知の数は、大人・子どもそれぞれの入場チケット代金ですね。
大人のチケット代をx円、子どものチケット代をy円とします。
大人4人+子ども3人の家族はチケット代に18,000 円かかったので、
4x+3y=18,000 ・・・①
大人2人+子ども2人の家族はチケット代に10,000 円かかったので、
2x+2y=10,000 ・・・②
①と②を連立させて解くと、
(x,y)=(3,000,2,000)
答えは大人1人3000 円、子ども1人2000 円となります。
(3) 身近な例から、連立方程式を考える癖をつけよう
身近なところにも連立方程式が関係していると、わかったでしょうか。こうした身近な例から考えていくと、親しみを持ちやすく、具体的にイメージしながら立式できるようになります。
「あるホームセンターでは、A洗剤3本とB柔軟剤を3本がセットで4,500円。別のドラッグストアでは、同じA洗剤4本とB洗剤5本がセットで6,500円。いったいどちらがお得なの?」…、と保護者の方が悩む問題も、連立方程式で解くことができます。
数学が苦手な生徒ほど、身近な例を思い浮かべ、解く練習を重ねてみてください。いつか、連立方程式をスイスイ解ける日が来るはずです。
「やる気が出ない」「やり方がわからない」、そんなときは遠慮なく塾の力を借りると良いでしょう。
連立方程式をマスターするならここ!おすすめの塾5選

基礎から発展問題、高校受験レベルまで、連立方程式で出題される問題は多彩です。連立方程式をマスターするには、プロのサポートを受けるのが近道。
ここからは、連立方程式をはじめ、中学生の数学対策におすすめの塾を5選紹介します。
(1) 個別教室のトライ
個別教室のトライは、全国に650の直営教室を展開する大手塾です。すべての教室で完全マンツーマンの授業を提供しており、指導する講師の質にも定評があります。
マンツーマン指導のメリットは、何といっても徹底的に生徒に合わせられること。問題文を読みながら一緒に方針を考えたり、計算過程を一つひとつを確認しながら進められたりと、つきっきりで指導してもらえます。連立方程式が苦手、あるいは中1の方程式から理解不足が積み重なっている中学生も、基礎からじっくりと克服できるでしょう。
お近くに個別教室のトライがない方には、オンラインでの指導がおすすめです。トライのオンライン個別指導塾は、トライの対面指導と遜色のない品質の授業をオンラインで受講できます。
個別教室のトライの料金情報は、以下のとおりです。
| 入会金 | 11,000円 |
| 授業料(目安) | 中学生 26,000円~30,000円/月 |
| その他の費用 | 季節講習あり(中学生は35,000円~70,000円程度) ※ 教材費は不要 |
料金を問い合わせる(ご利用無料)
(2) 東京個別指導学院・関西個別指導学院
ベネッセグループの塾である東京個別指導学院・関西個別指導学院は、情報収集力と分析力を生かした、緻密な指導で人気を集めています。
中学生が連立方程式でつまずく原因も知り尽くしており、苦手意識を克服させた実績も多数。講師が生徒に頻繁に問いかける対話型授業は、中学生に「自分で考える力」「試行錯誤する力」を養成します。「自分で問を立て、自分で考える力」は、連立方程式以外の数学や、他教科にも良い影響を与え、5教科の総合力が伸びることも期待できるでしょう。
部活や習い事とも両立しやすい、自由な時間割も東京個別指導学院・関西個別指導学院の特徴です。お子さんのペースに合わせ、コツコツと数学に取り組みたい方に向いています。
東京個別指導学院・関西個別指導学院の料金情報は、以下のとおりです。
| 入会金 | なし |
| 授業料 | 受講教科や回数、ペース、使用教材などによって変動 要問合せ |
| その他の費用 | 季節講習あり |
料金を問い合わせる(ご利用無料)
(3) 個別指導WAM
個別指導WAMは、中学校の定期テストに合わせて数学対策を進めたい方におすすめです。全国に展開する教室は、どれも地域に密着。中学校別の授業進度やテスト範囲、出題傾向に合わせた的確な指導が受けられます。
指導する講師は難関大生やプロ講師など、数学指導に熟達した人材ばかり。経験と親しみやすさを兼ね備えており、分からない点をいつでも気軽に質問できると評判です。中1・12⽉〜中3・4月に入会した中学生を対象にした成績保証制度は、個別指導WAMの指導力あってこそのサービスでしょう。
お近くに個別指導WAMの教室がない場合は、オンライン指導を検討してみましょう。オンライン家庭教師WAMは、個別指導WAMが培ったノウハウをオンラインで受講できるサービスです。
個別指導WAMの料金情報は、以下のとおりです。
| 入会金 | 入会金と登録料が必要、金額は要問合せ |
| 授業料 | 中1・2→7,600円~ 中3→8,400円~ ※週1回・40分コースの月額 |
| その他の費用 | 年会費 維持管理費(毎月) e-ラーニング教材費 |
※ 返金制度あり
最短1分で完了! 個別指導WAMのお近くの教室に料金を問い合わせる(ご利用無料)
(4) 代々木個別指導学院
代々木個別指導学院では、生徒一人ひとりに徹底的に合わせた指導を受けられます。
相性を慎重に考慮して決まる担当講師が、お子さんの思考に合わせて丁寧に指導。連立方程式の考え方や解き方、典型問題のアプローチ法など、テストの正答率を上げるポイントを細かく教えてくれます。
また、代々木個別指導学院は、生徒の自立心も大切にします。一から十まで教えず、生徒が自分で考え、自分の力で取り組む時間を確保するのも、自立してほしいという思いのあらわれ。これまでにも、講師のサポートを受けながら徐々に自分で取り組めるようになり、定期テストや受験で目標を達成した先輩が続出しています。
代々木個別指導学院の料金情報は、以下のとおりです。
| 入会金 | 20,000円 |
| 授業料 | 10,800円~/1科目 |
| その他の費用 | 季節講習あり(30,000円~40,000円程度) |
料金を問い合わせる(ご利用無料)
(5) ナビ個別指導学院
ナビ個別指導学院は、中学生の勉強に欠かせない「モチベーション」を上げる塾です。モチベーションを上げる秘訣は、講師の「褒め力」。褒め研修を受けた講師が、生徒の成長や努力をつぶさに見つけ、承認します。褒められた生徒は自己肯定感が高まり、やる気になり、自主的に勉強に向かえるようになるというわけです。
授業では、ナビ個別指導学院専用に開発されたオリジナル教材「ナビスタ!」を使います。つまずきやすいポイントや、ライバルに差をつけられる問題を精選した教材で、苦手な連立方程式も本質的に理解できるようになるでしょう。教室には自習室も完備。塾の課題や学校の宿題、テスト勉強、受験勉強にと、自然と行きたくなる学習空間として活用できます。
ナビ個別指導学院の料金情報は、以下のとおりです。
| 入会金 | 22,000円 |
| 授業料 | 中1・2→12,600円 中3→16,800円 ※ 週1回授業を受けた場合の月額 |
| その他の費用 | 諸経費 3,480円/月 季節講習あり(コマ単価3,700円~3,800円) |
料金を問い合わせる(ご利用無料)
まとめ
この記事では、連立方程式の2つの解法、文章題でよく問われる典型パターン例題、難しいとされる理由と対策、勉強方法について解説しました。
連立方程式は高校入試でもかならず出題される、中学数学で最重要な単元の1つです。
計算そのものの難度は高くないものの、文章題に苦戦する中学生が続出します。とくに「割合」「速さ」などは、頻出の典型問題であるにもかかわらず、得点できないケースがよくあります。
割合や速さの連立方程式を解くためには、小学校で学習した内容の理解も欠かせません。塾や家庭教師の力を借りつつ、忙しい合間を縫って効率的に復習と習得ができるよう学習計画を立てましょう。
個性や思考タイプに合った塾・家庭教師を探すには、「塾探しの窓口」の利用がおすすめです。お子さんの学年とお住まいのエリアを選択するだけで、利用者からの口コミ評価が高いサービスを瞬時に選定します。また実際に通った人の口コミを見ながら、お近くの塾を選定できます。
「塾探しの窓口」のご利用は無料で、会員登録もいりません。まずは気軽に、お近くの塾を探してみてくださいね。



中学生向けのおすすめ塾
中学生向けの塾の料金・口コミ
- 個別教室のトライの料金・口コミ
- 東京個別指導学院・関西個別指導学院の料金・口コミ
- 代々木個別指導学院の料金・口コミ
- 個別指導WAMの料金・口コミ
- ナビ個別指導学院の料金・口コミ
- 中高一貫校専門 個別指導塾WAYSの料金・口コミ
- スタディコーチの料金・口コミ
- 坪田塾の料金・口コミ
- 個別指導塾トライプラスの料金・口コミ
- 個別指導学院サクシードの料金・口コミ
- 個別指導スクールIEの料金・口コミ
- 個別指導塾スタンダードの料金・口コミ
- 個別指導塾サクラサクセスの料金・口コミ
- ドリームホームスクールの料金・口コミ
- みやび個別指導学院の料金・口コミ
- ITTO個別指導学院の料金・口コミ
- コノ塾の料金・口コミ
- 学習空間の料金・口コミ
- キズキ共育塾の料金・口コミ
- 森塾の料金・口コミ
- 自立学習REDの料金・口コミ