学習塾の口コミ比較サイト「塾探しの窓口」が運営。初めて塾を探されている保護者に向けて、塾を探す上での基礎知識や塾選びを成功に導くためのポイント等を、わかりやすくお届けします。
【中2数学】1次関数を習得せよ!基本から入試レベルまで

「変化の割合=xの増加量分のyの増加量」と暗記だけして、本番で解けないと困っていませんか?あるいは「点Pが嫌い」「水槽の問題はお手上げ」という中学生もいるでしょう。
中学生に数学の苦手分野を聞くと多くの生徒が「1次関数」と答えます。苦手とする人が多いにもかかわらず、定期テストや高校入試では頻出のため逃げるわけにはいきません。
この記事では1次関数を、考え方の基本の基本から丁寧に解説します。典型的な問題の解き方や、1次関数が得意になれる勉強のコツもまとめました。
まず「1次関数とはそもそも何なのか」から、一緒に考えていきましょう。記事を読み終わるころには、きっと「1次関数、勉強してみようかな」と思えるようになっているはずです。
「1次関数」とは

1次関数の前に、関数とは何か確認しておきましょう。
関数とは「xとyという2つの実数があったとき、xの値が決まるとyの値も1つに決まる関係」を指します。xの値次第でyの値が決まる関係のことを「yはxの関数である」といいます。
中1で習った関数「正比例」「反比例」を思い出してみましょう。グラフを描く際、xの値に対応するyの値をとり、線で結んでいきましたね。この関係が、関数です。
中2で習う1次関数は、関数のうち「yを、xの1次式」で表せるものの総称です。xの1次式とは、xが1回だけ掛けられている式を指します。
1次関数の式は、以下のとおりです。
aを「傾き」「変化の割合」、bを「切片」と呼びますが、詳しくは次の章で解説します。
また実は、比例は1次関数の1種です。1次関数の式y=ax + bにおいてb=0、つまり切片が原点である関数を、特別に「比例」と呼びます。
実は関数は、1次関数以外にもさまざまあります。中3では「2次関数」を習い、高校数学では3次関数が登場します。なかでも、中2で習う1次関数はさまざまな問題が作りやすく、入試でも頻出の単元です。1次関数の基本と、応用問題にあたる「1次関数の利用」までしっかりマスターしましょう。
1次関数の基本を理解しよう

続いて、1次関数 y=ax + bの基本的な事項を確認しましょう。1次関数を苦手とする中学生の中には、これから解説する基本が十分理解できていないケースもよく見られます。
「aとは何か」「bとは何か」など、自分の言葉で説明できる状態を目指しましょう。
(1) 切片「b」とは
切片bとは、1次関数y=ax + bのグラフがy軸と交わる点を指します。
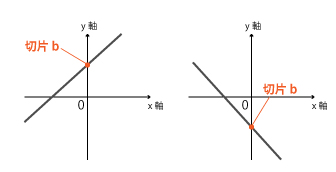
y軸との交点、つまり「xが0」のときのyの値です。よって切片bを求めたい場合は、y=ax + bにx=0を代入すればOKです。
(2) 変化の割合「a」とは
1次関数の理解でさらに重要なのが「a」です。aは「傾き」「変化の割合」と呼ばれます。
「傾き」…x が1増えたときにyが変化する量
「変化の割合」…xの値を変化させたとき、どのくらいyの値が変化するのかの割合
この2つは、1次関数においては同じものを指しています。ただし「傾き」は1次関数だけで使われる概念です。中3の2次関数では使いませんので、注意しましょう。
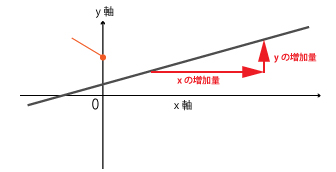
変化の割合は「xの増え方によって変化するyの値の割合」を示すため、次の式で表されます。
a=yの増加量/xの増加量
(3) 変域
変域はxとy、それぞれに設定されます。とくに「グラフを描く問題」「1次関数の利用の問題」でよく登場するため、しっかり理解しておきましょう。
たとえば速さや水量の増加などに関する問題は、xとyで設定される値が「正の数」をとります。「負の速さ」「負の水量」はありえないためです。このとき、xやyがとる値は整数であることを示すために、変域「x≧0」「y≧0」と書かれます。
これが変域です。
変域は問題によって設定される範囲が異なるため、注意深く問題文を読み正しくつかむようにしましょう。
1次関数をグラフで理解しよう

1次関数の始まりは、グラフを描くところから始まります。比例との違いにも注意しつつ、グラフを正しく書けるよう練習してみてください。
1次関数のグラフの書き方を解説します。
(1) 1次関数のグラフ
1次関数のグラフは右上がり、もしくは右下がりの直線になります。
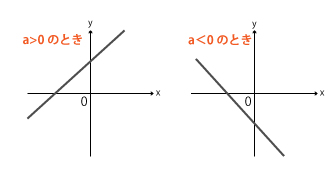
変化の割合aが負の場合、xが増加するにつれてyは減少するためグラフは「右下がり」になります。
切片b=0だと原点を通るグラフになり、比例になることは前述しました。
(2) 1次関数のグラフの書き方
1次関数のグラフの書き方は、以下の手順で進めます。
2. 切片bをy軸上に設置します。
3. 直線にするため、もう1点を設置します。
4. 2点を通る直線を引きます。
切片はy=ax + bの式を見ればわかりますね。bの値をy軸上に置くだけです。もう1点を簡単にとるには、x軸との交点(y=0)を使うのがおすすめです。
例題を使って理解しましょう。
| <例題> y=2x+6のグラフをかけ。 |
式より、切片bが6だとわかります。またx軸との交点、つまりy=0のときのxの値は、次のとおりです。
2x+6=0
2x=-6
x=-3
したがってx軸との交点は(-3,0) グラフは次のようになります。
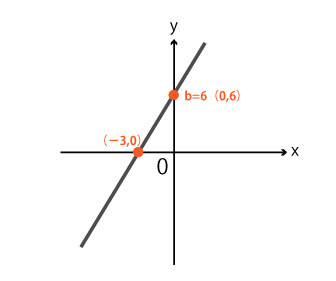
まずはさまざまな1次関数のグラフを描き、慣れてください。
1次関数の基本問題をマスターしよう

基本のグラフが書けるようになったら、やや発展させた練習問題に進みましょう。定期テストや高校入試でかならずといって良いほど出る問題は、次の4種類です。
・変化の割合を求める問題
・yの増加量を求める問題
・グラフから式を求める問題
・与えられた値から式を求める問題
どれも1次関数を本質的に理解するのにぴったりの問題ばかりです。一つひとつ、解き方や考え方を丁寧に解説しますので、じっくり見てみてください。
(1) 変化の割合を求める問題
変化の割合を求める問題は、次のように出題されます。
| <例題> xの増加量が3、yの増加量が-12のときの変化の割合を求めよ。 |
この問題はxとy、それぞれの増加量が与えられています。そのため、変化の割合の式に代入すれば解けます。
<解き方>
問題文で与えられた「xの増加量が3、yの増加量が-12」を、変化の割合を表す式
変化の割合=yの増加量/xの増加量
に代入する。
変化の割合=-12/3
したがって、変化の割合=-4
(2) yの増加量を求める問題
yの増加量を求める問題は、次のように出されます。
| <例題> 1次関数y=2x+3において、xが1から7まで増加する場合のyの増加量を求めよ。 |
これはxの変化が与えられ、対応するyの変化を求めさせる問題です。逆のパターン(yの変化が与えられ、対応するxの変化を求めさせる問題)もあります。
<解き方>
1次関数の式はy=2x+3なので、変化の割合a=2だとわかります。
変化の割合=yの増加量/xの増加量
なので、今回求めたいyの増加量に合わせて式を変形すると、
yの増加量=変化の割合×xの増加量
また問題より、xの増加量は7-1=6なので、式にあてはめると
yの増加量=2×6
したがって、yの増加量=12
(3) グラフから式を求める問題
グラフが与えられ、式に表すよう求める問題もあります。
| <例題> 次の直線の式を求めなさい。 |
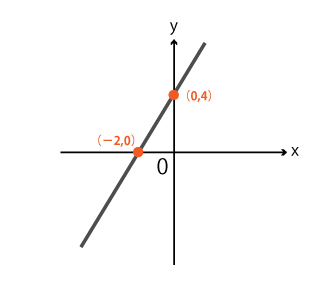
まず、y軸との交点に注目します。y軸とグラフとの交点は「切片b」でしたね。
問題のグラフからb=4とわかるため、式は次のようになります。
y=ax+4
次に知りたいのは変化の割合(傾き)aです。aは「yの増加量/xの増加量」で求められましたね。
x軸との交点から切片までの間に、xは2増えています。一方yは4増えています。したがって、
変化の割合a=4/2
a=2
以上を1次関数の式に表しましょう。
答え y=2x+4
(4) 与えられた値から式を求める問題
1次関数の基本問題には、与えられた値から式を求める問題もあります。例を見てみましょう。
| <例題> 2点(2,-2)(-1,7)を通る直線の式を求めなさい。 |
このタイプの問題はそれぞれの値をy=ax + bに代入し、連立方程式として解いてaとbを求めます。
<解き方>
(2,-2)をy=ax + bに代入すると、
2a+b=-2 …①
(-1,7)をy=ax + bに代入すると、
-a+b=7 …②
①と②を連立方程式として解くと、a=-3、b=4
答え y=-3x+4
1次関数の発展問題をマスターしよう

いわゆる応用問題にあたる「1次関数の利用」の前に、もう2つだけマスターしておきたい問題があります。x軸、y軸との交点の求め方と変域の求め方です。
順番に確認していきましょう。
(1) 式からx軸、y軸との交点を求める問題
x軸、y軸との交点は何かと使う頻度が高いポイントです。サクッと正確に求められるようにしておきましょう。
| <例題> 1次関数 y=1/3x+2の、x軸、y軸との交点の座標をそれぞれ求めよ。 |
<考え方>
x軸との交点は「y=0」のときのxの値を指します。
1次関数の式にy=0を代入して、
1/3x+2=0
1/3x=-2
x=-6
またy軸との交点は「x=0」のときのyの値でした。1次関数の式にx=0を代入しても解けますが、y軸との交点=切片bであることを思い出しましょう。
つまり1次関数の式に最初から切片bが示されているということです。
1次関数の式はy=1/3x+2、つまりy軸との交点は(0,2)
答え、x軸との交点(-6,0) y軸との交点(0,2)
(2) 変域を求める問題
基本的な練習問題は、この変域を求める問題で最後です。変域の考え方と求め方をまとめてチェックしておきましょう。
| <例題> 1次関数y=-3x+2において、xの変域が-2≦x≦1である。このときのyの変域を求めよ。 |
変域を求める問題は、xとyの変域の対応を正しく組み合わせることが大切です。「xがいくつのときにyが最大・最小をとるか」は、グラフの傾きをイメージするとつかみやすくなります。
<考え方>
まず、与えられたy=-3x+2のグラフはどのような形になるかを考えましょう。
y=-3x+2は傾きaがマイナスのため、右下がりの形状を取ります。
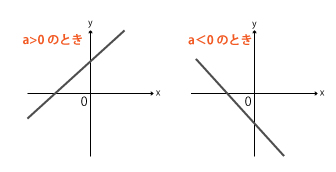
右下がりのグラフは「xの値が増加すると、yの値は減少」しますね。したがって、xが最小のときyは最大値をとり、xが最大のときyは最小となります。
この点を踏まえて変域-2≦x≦1を、1次関数の式y=-3x+2に代入してみましょう。
x=-2のときは、
y=-3×(-2)+2
y=8
x=1のときは、
y=-3×1+2
y=-1
したがってyの変域は、-1≦y≦8となります。
1次関数の利用(文章題)をマスターしよう

ここからは1次関数の最大の難所、文章題の考え方・解き方を解説します。
実は1次関数の文章題は、変化する2つの数があれば事象の数だけ作れます。私たちの身の回りにあるあらゆる要素が、1次関数の題材になるといっても過言ではありません。
問題作成のバリエーションが豊富で、受験生がこれまでに見たことがないような問題を作りやすいというのも、高校入試で1次関数が頻出する理由の1つです。
とはいえ、典型的な問題もあります。ここでは4つの典型的な1次関数の問題を取り上げ、アプローチ法を解説します。
(1) ばねの伸びの問題
「おもりの重さ」と「ばねの伸びの長さ」に関連性のあるばねは、一次関数の利用のなかでも基本として出題されやすい問題です。
| <例題> ばねの伸びる長さは、つるしたおもりの重さに比例する。このことを踏まえて、次の問題に答えよ。 1. おもりの重さをxg、ばねの伸びをycmとする。あるばねに重さを変えながらおもりをつるしていったところ、下の表の結果が得られた。この表のxとyの関係を式に表せ。 2. このばねに9gのおもりをつるしたときの、ばねの伸びは何cmになるか。 |
| おもりの重さ(xg) | 0 | 2 | 4 |
| ばねの伸び(ycm) | 9 | 11 | 13 |
<考え方>
1. 問題文において「ばねの伸びる長さは、つるしたおもりの重さに比例する」と書かれているため、これは1次関数の問題だと考えます。
(比例の問題だったとしても、比例は切片b=0の1次関数とみなせるため、1次関数の解き方で解けます。)
1次関数の式y=ax + bを思い浮かべ、表の値を代入していきましょう。
ちなみにaとbの2つの文字を求める必要があるため、連立方程式で解くのが基本です。
ただし今回の問題は「x=0」のときのyが与えられている点に注目しましょう。x=0のときのyの値には、特別な名前が付いていました。覚えていますか?
そうです、「切片b」です。
つまり「x=0」のときy=9であるため、
切片b=9
がわかります。
これで求める式はy=ax + 9となり、残る文字はaのみとなります。
y=ax + 9に、x=2、y=11を代入してみましょう。
a×2+9=11
2a=2
a=1
したがって傾きa=1であるため、1次関数の式が求められました。
答え y=x+9
2. 1で表の1次関数はy=x+9だとわかりました。
この式にx=9を代入すると、
y=9+9
答え ばねの伸びは18cm
xとyで示された値を丁寧に見て、間違えずに代入していきましょう。
(2) 点Pと面積の問題
続いての問題は、四角形の辺上を点Pが移動する問題です。Pの位置によって形成される図形の形が変わるため、図を描くと解きやすいでしょう。
| <例題> 図のような長方形ABCDがある。長方形ABCD上には点Pがあり、点PはAを出発し、毎秒1cmの速さで、長方形の周上をAからDまで移動する。 このとき、点PがAを出発してx秒後の△APDの面積をy㎠とする。 点Pが辺BCにあるときのyをxの式で表せ。 |
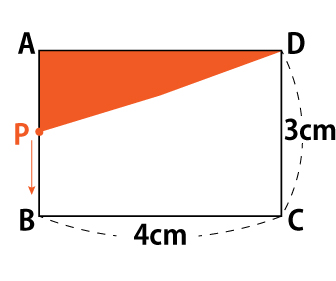
<考え方>
まず、何はともあれ指定された状況の図を描いてみましょう。問題文の図では点PはAB上を移動していますね。同じようにBCを移動している点Pを描いてみてください。
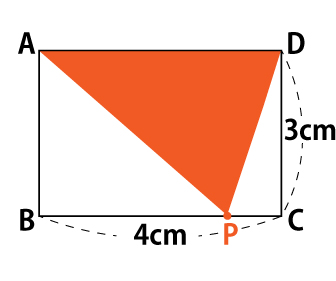
図はこのようになります。
さて、求めるべきは△APDの面積y㎠ですね。△APDは底辺AD=4cm、高さDC=3cmのため、
y=1/2×4×3
y=6
答え y=6
今回、xはAを出発してからの経過秒数を示しています。また速さは毎秒1cm、つまり「1秒で1cm」進みます。
したがってxの変域は以下のようになります。
・ABにあるとき 0≦x≦3(0秒から3秒後まで)
・BCにあるとき 3≦x≦7(3秒後から7秒後まで)
・CDにあるとき 7≦x≦10(7秒後から10秒後まで)
点Pの問題と変域はセットで出題されることが良くあります。変域の考え方も確認しておいてください。
(3) 速さと距離の問題
苦手とする中学生が多くいるのが、1次関数を利用した速さの問題です。
| <例題> 自宅から3000m離れた駅まで、途中の駐輪場までは自転車で行き、駐輪場からは歩いて移動した。駐輪場までは15分、2700m、駅までは20分かかった。x分後の道のりをymとして、問に答えよ。 1. 自転車に乗っているときの速さを求めよ。 2. 駐輪場から駅までのyをxの式で表せ。 |
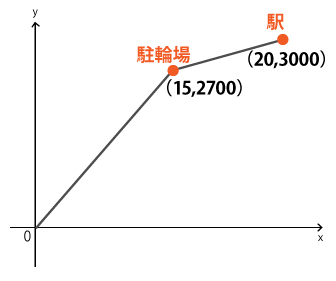
<考え方>
1. 求めるのは「速さ」です。速さは、どのように表わされましたか?
速さ=道のり/距離
ですね。
今回の問題では「駐輪場までの道のりは2700m」「かかった時間は15分」と明示されています。この2つの数値を、先ほどの速さの公式に当てはめましょう。
速さ=2700/15
答え 180m/分
2. 問題文より、
y=駐輪場から駅までの道のり
x=駐輪場から駅までかかった時間
とされています。
またグラフを見ると、1次関数であるとわかります。最終的に示す式の形はy=ax + bとなるため、与えられた数値からaとbを求めましょう。
駐輪場の座標(15,2700)と駅の座標(20,3000)それぞれをy=ax + bに代入します。
15a+b=2700 …①
20a+b=3000 …②
①②を連立方程式にして解きましょう。
②-①で
5a=300
a=60
a=60をy=②に代入し、
20×60+b=3000
1200+b=3000
b=1800
答え y=60x+1800
基本的な問題を繰り返し解き、コツをつかんでください。
(4) 水槽に水を入れる問題
水槽に水を入れる問題は、さまざまなパターンがあります。すべての水槽問題の基本となる考え方を習得しましょう。
| <例題> 満水になると90リットル入る水槽に、20リットルの水が入っている。ここにこれから毎分8リットルずつ水を入れる。水を入れ始めてからx分後の水槽の水の量をyリットルとし、yをxの式で表せ。 |
<考え方>
まず、与えられている要素を整理しましょう。
・90リットルで満水
・はじめに20リットル入っている
・毎分8リットルずつ水が増える
またxとyはそれぞれ以下です。
・x 水を入れ始めてからの経過分数
・y 水槽に溜まった水の量
さてx分後の水の量は「もともと入っていた20リットル+x分間に増えた水の量」で表せます。「x分間に増えた水の量」とは、つまりyです。
たとえば1分後には8リットル×1分=8リットルが増えます。
2分後なら8リットル×2分=16リットル増えることになります。
つまり、x分後なら8×x分=8xリットル増えるわけです。
y=もともと入っていた20リットル+x分間に増えた水の量ですから式にすると、
答え y=8x+20
わからなくなったら、1分後と2分後を考えてみましょう。1分後と2分後の関係性からx分後が表せれば、解けたも同然です。
1次関数の理解が重要な2つの理由

1次関数は、とても大切な単元です。中学校の先生にも繰り返し、「1次関数は重要だ」「しっかり勉強するように」といわれていないでしょうか。
1次関数が重要な理由を2つ、解説します。1次関数の意義を理解し、勉強へのモチベーションとしてください。
(1) 高校入試で大問として出題される
1次関数は、高校入試でかならずといって良いほど出題されます。それも、大問として15~20点分もの配点を持っている試験も、少なくありません。
実際、2025年度の東京都立高校入試では、1次関数(融合問題を含む)で15点分が出題されています。1次関数の発展単元である2次関数と融合させた問題、図形と組み合わせた問題も、頻繁に出されています。
1次関数は順序立て、物事を論理的に考えられる力を測るのに、最適な単元です。また、多様な問題を作成しやすく、初見の問題に対する受験生の対応力も測れます。
こうした理由から、高校入試では1次関数が必出となっています。第一志望校合格をめざす中学生にとって、1次関数は避けて通れない関門なのです。
(2) 高校数学につながる知識が詰まっている
1次関数は、「関数」分野の基本となる単元です。2次関数、3次関数と発展していく関数を理解するための基本が詰まっており、高校数学への円滑な移行に重要な役割を果たします。
また、内容の抽象度が高まる高校数学に向けて、さまざまな事象を数理的・抽象的にとらえ、理解する力も養成します。問題に向き合い、論理的に解決する力を育てられれば、数学だけではなく、高校のあらゆる学びに役立ちます。
1次関数は中学生の思考力を、高校受験を経て高校生レベルに育てる、そのエッセンスが詰まった単元だと考えてみてください。
1次関数が得意になれる勉強法

1次関数は定期テストや高校入試で、問1の小問としても・大問としても出題されます。それだけ重要な単元という意味を持っているためです。
出題頻度が高い1次関数を習得できれば、点数の大幅アップも夢ではありません。
1次関数を得意にする勉強法を、4つの視点から解説します。
(1) 式の意味、グラフがあらわす事象を理解しようとする
1次関数は、xとyとの異なる値の関係性を式に表したものです。つまり大切なのは「関係性」だという点を見逃してはいけません。
中学生はつい、目先の計算に真剣になるあまりに1次関数の本質を見落としているケースがあります。式やグラフが表している意味、要素の関係性をしっかり考えるようにしましょう。
同様に「変化の割合はxの増加量分のyの増加量」と呪文を暗記しても、問題は解けません。
「変化の割合とは何か」「なぜ『xの増加量分のyの増加量』で算出できるのか」といった根本的な理解を大切にしましょう。
(2) 典型パターンの問題を反復し、考え方を身につける
記事で紹介したように、1次関数にはいくつかの典型問題があります。「変域を求める問題」「速さの問題」などが代表例です。
典型問題は、あらゆる場面でよく出題されるからそう呼ばれるのです。典型問題を数多く練習し、解き方をマスターしてください。
良質な典型問題が豊富に載っているのは学校のワークです。学校で配布された中2ワークの「1次関数」を、最低3回繰り返してみましょう。
(3) 文章題は「変化する量」と「その関係性」を式にする
1次関数の利用と呼ばれる文章題が難しいのは、問題文の長さによって変化する量や関係性を見つけにくくなっているためです。文章題を解く際は不要な情報を極力そぎ落とし、「変化する量」と「その関係性」だけを抽出してみてください。
また自分がいま何を考えているのか、迷子になりやすい点にも注意します。xを求めているのかyを求めているのか、あるいは立式したいのか値をもとめたいのかなど、求めたい結果を意識しながら解き進めることを忘れないようにしましょう。
(4) 塾や家庭教師の力を借りる
1次関数を完成度高く習得したい場合、独学では難しいかもしれません。1次関数はそれほどに奥深く、難しい単元だからです。
もし自分の力で1次関数の学習を進めるのは難しいと感じたら、遠慮なく塾や家庭教師の力を借りましょう。本質をわかりやすく解説してくれるため、目の前のもやがスッと晴れる実感を得られるはずです。
また1次関数の苦手は、根本的に比例の理解不足や方程式の習熟度不足に起因する場合もあります。単元を超えての原因追及は、中学生には難しいかもしれません。塾や家庭教師を利用すると別の単元の習得度不足も見つけてもらえ、数学全体の実力底上げが期待できます。
身の回りにある1次関数

「動く点P」「栓をしていない水槽」「逃げる弟を追いかける兄」といった、1次関数の典型問題は、問題の場面設定に無理があります。「そんなこと、ありえない」と、無意識に脳が問題を拒絶し、理解を妨げている可能性もゼロではないでしょう。
もっと身近で、理解しやすい1次関数の例を見てみませんか。「そうか、これも1次関数か」「1次関数とは、こういうことか」と腹の底から納得でき、1次関数の単元理解が進むかもしれませんよ。
(1) コンビニでペットボトルを買おう
「コンビニでペットボトル入り飲料を買う」、よくあるシチュエーションです。いまは、どのコンビニも、レジ袋をもらうと1枚3円ほどかかります。この場面を考えてみましょう。
さて、ペットボトル1本を150円としたとき、代金はどう表せますか?
代金=150円×1本+レジ袋3円
ですね。
では、友だちや先輩に頼まれ、x本のペットボトルを買うと考えてください。この時の代金yは、どう表せるでしょうか。
代金y=150円×x本+3円
→ y=150x+3
どうでしょう、見事に1次関数となりました。1次関数は、これほどまで身近な場面にひそんでいるのです。少し、興味がわいてきましたか?
(2) 電気料金を考えてみよう
電気料金は、電力会社によってさまざまなプランがあります。ただ、使い放題というプランはありません。どのプランも、使用量に応じて料金が増えるシステムになっています。
また、電気料金には「基本料」といい、電気の使用有無にかかわらず請求される料金があります。電気を使う権利料と考えても良いでしょう。
さて、あなたの家の電気料金は、どのような式で表せるでしょうか。
支払う電気料金=基本料+1kWhあたりの電気量単価×電気使用量
支払う電気料金をy円、基本料を1500円、1kWhあたりの単価を30円、使用量をxkWとして、上記の式を書き換えます。
支払う電気料金y円=基本料1500+単価30円×使用量x
→ y=30x+1500
どうでしょうか。こちらも1次関数になりました。
(3) 社会で活用される1次関数
コンビニでの買い物や電気料金のほかにも、1次関数は以下のような場面で活用されています。
・上下水道料金
・移動距離の計算
・データ分析
・年収計算
・金利計算 など
1次関数は変化する数量の関係性を表す基本的な概念として、社会で欠かせない理論となっています。もし1次関数が苦手なら、身近な例を探してみてください。動く点Pや栓がされていない水槽よりも、親しみやすく、理解しやすい事例が見つかるかもしれませんよ。
【中2数学】1次関数のマスターにおすすめの塾5選

1次関数は、多くの中学生がつまずく難関です。さまざまな数学力が複雑に絡み合うため、自力での克服は難しいかもしれません。
1次関数に困っていたら、塾を利用してみませんか。プロの指導でサクッと克服できれば、あまった時間を別の学習に回せるようになります。1次関数の学習に自信をもっておすすめできる個別指導塾を5つ紹介します。
個別教室のトライ
個別教室のトライは、講師1人に生徒が1人のマンツーマン指導を徹底する塾です。
教室には「トライさん」と呼ばれる教育のプロ(教育プランナー)が常駐し、学習のあらゆる相談に対応します。トライさんとの面談を通じて1次関数が苦手になった原因を究明し、無理なく進める学習計画を立て、マンツーマンでじっくりと学び克服する。そんな理想的ともいえる学習ストーリーも、個別教室のトライならお手のものです。
トライグループは、講師人材の厚みも魅力の1つ。総登録講師数はなんと33万人、お子さんと相性の合う講師が、きっと見つかります。
お近くに個別教室のトライがない場合は、トライのオンライン個別指導塾をご検討ください。自宅にいながら、トライ品質の授業を受けられるオンラインサービスです。
個別教室のトライの料金情報は、以下のとおりです。
| 入会金 | 11,000円 |
| 授業料(目安) | 中学生 26,000円~30,000円/月 |
| その他の費用 | 季節講習あり(中学生は35,000円~70,000円程度) ※ 教材費は不要 |
無料資料請求する
東京個別指導学院・関西個別指導学院
東京個別指導学院・関西個別指導学院は、生徒一人ひとりに最適な学習計画の立案と講師選定にこだわる塾です。学習計画は現状と目標を精緻に分析した上で、無理なく続けられるペースで策定。他の習い事や部活とも両立できるよう、通う曜日・時間帯を自由に選べます。
また、相性の合う講師と楽しく学べるよう、本格的に授業が始まる前には、複数人の講師と体験授業をセッティング。お子さん自身が「この先生と頑張りたい」と思えた1人が担任になり、目標達成まで伴走します。
ベネッセグループの塾として、最新の教育情報の収集にも余念がありません。最新トピックや受験の傾向を踏まえた、的確な指導が期待できます。
東京個別指導学院・関西個別指導学院の料金情報は、以下のとおりです。
| 入会金 | なし |
| 授業料 | 受講教科や回数、ペース、使用教材などによって変動 要問合せ |
| その他の費用 | 季節講習あり |
無料資料請求する 最短1分で完了! 関西個別指導学院のお近くの教室に
無料資料請求する
個別指導WAM
「1次関数を克服して、学校のテストで結果を出したい」と考える中学生には、個別指導WAMをおすすめします。個別指導WAMは、全国に教室を展開する大手塾ながら、一つひとつの教室は地域の学校に密着。定期テストの傾向や難易度に合わせた、結果に直結する指導が受けられます。
独自の学習プログラムに沿って、実力派の講師陣が指導する授業は「面白い」「数学が好きになった」とのコメントが続出する充実度。個別指導の割にリーズナブルな受講料も見逃せません。数学に加えて英語や国語も受講し、実力の底上げも図れます。
自宅にいながら対面指導と同クオリティの指導が受けられるオンライン家庭教師WAMも人気です。お近くに個別指導WAMの教室がない方は、オンライン家庭教師を検討してみてください。
個別指導WAMの料金情報は、以下のとおりです。
| 入会金 | 入会金と登録料が必要、金額は要問合せ |
| 授業料 | 中1・2→7,600円~ 中3→8,400円~ ※週1回・40分コースの月額 |
| その他の費用 | 年会費 維持管理費(毎月) e-ラーニング教材費 |
※ 返金制度あり
最短1分で完了! 個別指導WAMのお近くの教室に無料資料請求する
代々木個別指導学院
苦手な単元の学習は、気が進まない中学生も多いでしょう。そんなときは、代々木個別指導学院に相談してみてください。代々木個別指導学院は生徒を褒めて励ましつつ、自立して勉強できる状態に導く指導を得意とする塾です。
めんどうみの良い講師と、「キミ専用カリキュラム」と呼ばれる自由度の高い学習計画で、苦手な1次関数もいつのまにかやる気になるはず。代々木個別指導学院が示す「何を、いつまでに、どのように勉強すれば目標を達成できるか」の計画で、先を見通せるようになり、勉強へのモチベーションも上がります。
代々木個別指導学院の料金情報は、以下のとおりです。
| 入会金 | 20,000円 |
| 授業料 | 10,800円~/1科目 |
| その他の費用 | 季節講習あり(30,000円~40,000円程度) |
無料資料請求する
ナビ個別指導学院
定期テストや高校受験は、自分一人の戦いです。自分の力で「できた!」といえる状態に完成させておくことが、最終的な成果を分けます。ナビ個別指導学院は、生徒の主体的な姿勢を育み、「自分でできた」と自信を持っていえるようにサポートしてくれます。
やる気を持って頑張れる秘密は、中学生指導に長けた講師の存在と、勉強しやすいオリジナルテキスト「ナビスタ!」。大事なポイントを丁寧に押さえながら進む授業は、わからなかった1次関数の世界が、クリアになる実感をもたせてくれます。
ナビ個別指導学院の料金情報は、以下のとおりです。
| 入会金 | 22,000円 |
| 授業料 | 中1・2→12,600円 中3→16,800円 ※ 週1回授業を受けた場合の月額 |
| その他の費用 | 諸経費 3,480円/月 季節講習あり(コマ単価3,700円~3,800円) |
無料資料請求する
まとめ
1次関数は中学数学でもっとも重要な単元の1つです。変化する数と関係性を見抜き式にするという数学的思考力を必要とする1次関数は、数学の実力を測る目的でよく出題されます。
大問として出されるケースも多いため、解ければ15点~20点の上乗せも不可能ではありません。
記事を参考に1次関数をしっかり理解し、典型問題の練習を通じて習得していきましょう。
1次関数のマスターにピッタリの塾や家庭教師を見つけるには「塾探しの窓口」をご利用ください。学年とお住まいの地域を入れるだけで、実際に利用した人からの評価が高い塾を簡単に見つけられます。



中学生向けのおすすめ塾
中学生向けの塾の料金・口コミ
- 個別教室のトライの料金・口コミ
- 東京個別指導学院・関西個別指導学院の料金・口コミ
- 代々木個別指導学院の料金・口コミ
- 個別指導WAMの料金・口コミ
- ナビ個別指導学院の料金・口コミ
- 中高一貫校専門 個別指導塾WAYSの料金・口コミ
- スタディコーチの料金・口コミ
- 坪田塾の料金・口コミ
- 個別指導塾トライプラスの料金・口コミ
- 個別指導学院サクシードの料金・口コミ
- 個別指導スクールIEの料金・口コミ
- 個別指導塾スタンダードの料金・口コミ
- 個別指導塾サクラサクセスの料金・口コミ
- ドリームホームスクールの料金・口コミ
- みやび個別指導学院の料金・口コミ
- ITTO個別指導学院の料金・口コミ
- コノ塾の料金・口コミ
- 学習空間の料金・口コミ
- キズキ共育塾の料金・口コミ
- 森塾の料金・口コミ
- 自立学習REDの料金・口コミ